1 引言
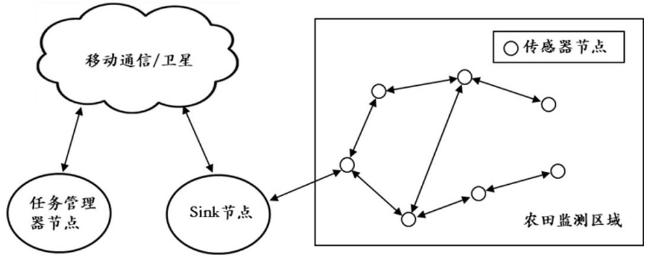
2 无线传感器网络结构
3 基于矩阵补全算法的节能优化算法
3.1 矩阵补全的基本原理
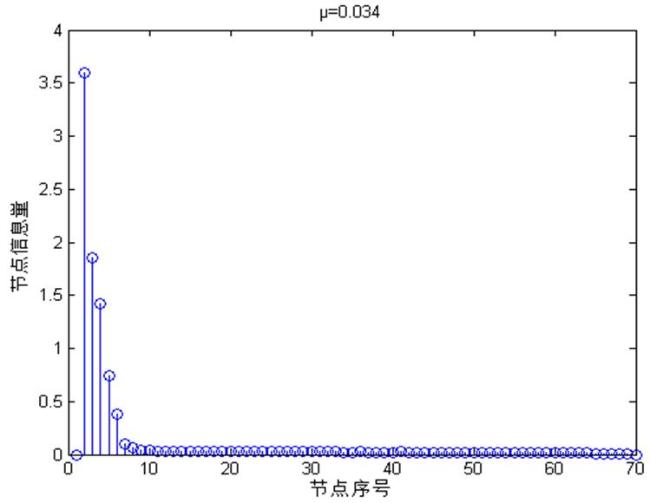
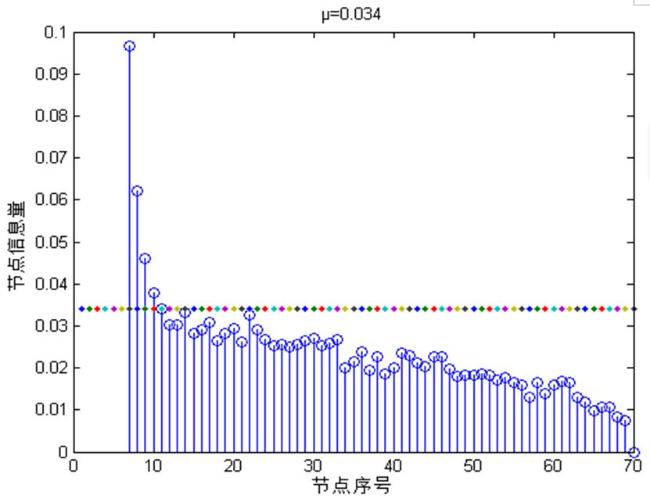
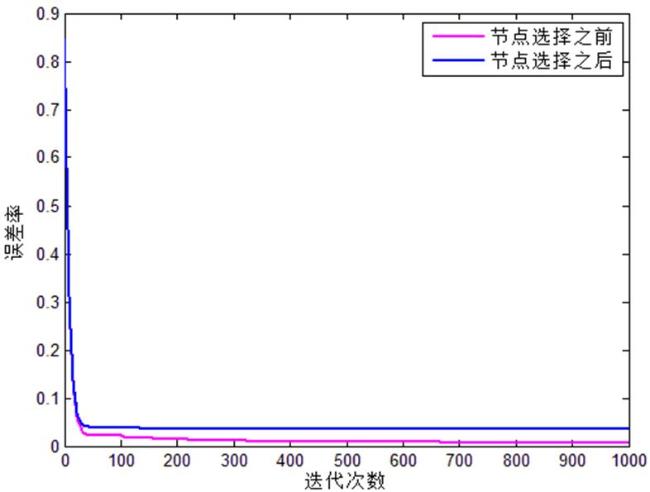
3.2 节点选择策略
表1 基于矩阵补全的传感器网络节点选择算法Table 1 Matrix completion based node selection algorithm for wireless sensor network |
| 1 | 初始化非冗余节点集Q_k:k=1,将任意一个节点加入到节点集,节点集中包含的节点数目n_k=1(n_k的最大值为NMAX),t=0 |
|---|---|
| 2 | 将节点集中节点的数据填充到原始数据矩阵中, |
| 3 | 以采样率对进行采样观测得到观测矩阵,采样集合为,其大小为 |
| 4 | 对运用矩阵补全算法得到恢复矩阵 |
| 5 | if then |
| 6 | 随机选择下一个节点且k增加1,将该节点数据和节点集中所有节点的数据都填充到新的原始数据矩阵中,并运用矩阵补全算法得到新的恢复矩阵 |
| 7 | 根据式(7)计算该节点的信息量 |
| 8 | if then |
| 9 | 将该节点加入到节点集中且增加1 |
| 10 | end if |
| 11 | ,返回第5步 |
| 12 | end if |