1 引 言
2 蔬菜价格影响因素分析
2.1 蔬菜价格影响因素
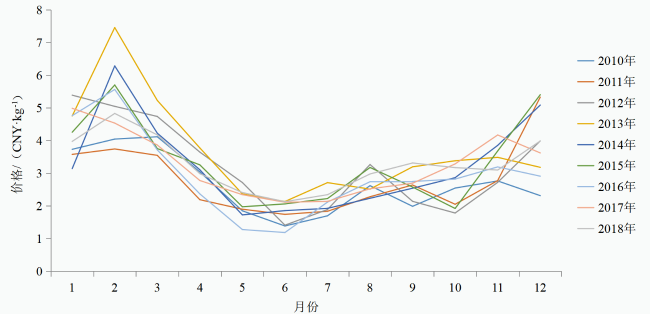
2.2 黄瓜价格波动分析
2.3 黄瓜价格影响因子
3 Lasso回归与BP神经网络结合的组合预测模型构建
3.1 理论基础
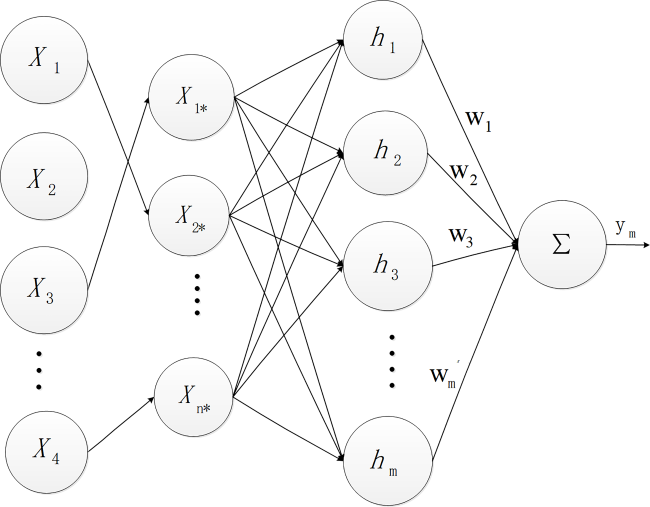
3.2 方法结合
3.3 数据标准化
3.4 基于Lasso回归的黄瓜价格影响因素选取
表1 Lasso回归模型变量选择与参数估计Table 1 Variable selection and parameter estimation of Lasso regression model |
| 系数 | 影响因素 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 播种面积 | 0 | -0.28212 | -0.20547 | -0.18647 | -0.19540 | -0.20108 | -0.20273 | -0.20646 | |
| 亩产量 | 0 | 0 | 0 | -0.18932 | -0.29021 | -0.10198 | 0 | 0 | |
| 受灾面积 | 0 | 0 | 0.408734 | 0.438949 | 0.445482 | 0.564859 | 0.592184 | 0.531208 | |
| 土地成本 | 0 | 0.239479 | 0.290850 | 0.303829 | 0.313982 | 0.360215 | 0.347498 | 0.324921 | |
| 物质与服务费用 | 0 | 0 | 0 | 0.101541 | 0.107532 | 0.140198 | 0.092192 | 0 | |
| 用工成本 | 0 | 0 | 0 | 0.386323 | 0.389201 | 0 | 0 | 0 | |
| 城镇居民人均可支配收入 | 0 | 0 | 0.523294 | 0.518713 | 0.514719 | 0.590234 | 0.364021 | 0.393297 | |
| 城镇居民人口数量 | 0 | 0.310583 | 0.210840 | 0.200987 | 0.112749 | 0 | 0 | 0 | |
| 城镇蔬菜消费价格指数 | 0 | 0.412385 | 0.354817 | 0.312390 | 0.378974 | 0.376213 | 0.374085 | 0.375532 | |
| 叶类蔬菜均价 | 0 | 0 | 0.570197 | 0.542760 | 0.423570 | 0.437502 | 0 | 0 | |
| 根茎类蔬菜均价 | 0 | 0.453750 | 0.421097 | 0.392375 | 0.321937 | 0.291374 | 0 | 0 | |
| 高速公路过路费 | 0 | 0 | 0 | 0.210870 | 0.124791 | 0.021397 | 0.078730 | 0 | |
| 燃油附加费 | 0 | 0 | 0 | 0.343019 | 0.341309 | 0.351035 | 0.253108 | 0.271075 | |
| 司机劳务费 | 0 | 0 | 0 | 0.039218 | 0.032957 | 0.023985 | 0.093213 | 0 | |
| 摊位费 | 0 | 0 | 0 | 0.196657 | 0.207866 | 0.251224 | 0.243317 | 0.213077 | |
| 人工费 | 0 | 0 | 0 | 0.217553 | 0.233591 | 0 | 0 | 0 | |
| 损耗费 | 0 | 0.353411 | 0.328929 | 0.293665 | 0.227755 | 0.236801 | 0 | 0 | |
| 包装加工费 | 0 | 0 | 0.217917 | 0.397591 | 0.319327 | 0.343109 | 0.327519 | 0.247327 | |
| 国家经济发展水平 | 0 | 0 | 0.153017 | 0.043092 | 0.039759 | 0.043197 | 0.022174 | 0 | |
| 人民币汇率 | 0 | 0 | 0.012874 | 0.023857 | 0 | 0 | 0 | 0 | |
| 通货膨胀率 | 0 | 0 | 0.565325 | 0.610128 | 0.540198 | 0.531208 | 0.531093 | 0.501098 | |
| 黄瓜产业扶持金额 | 0 | 0 | 0 | 0 | -0.320180 | -0.290180 | -0.341820 | -0.351080 | |
| 气温平均值 | 0 | -0.43296 | -0.532850 | -0.624810 | -0.619750 | -0.603290 | -0.593820 | -0.592190 | |
| 气温偏离正常值 | 0 | 0.431028 | 0.413098 | 0.323093 | 0.413902 | 0.532101 | 0.632181 | 0.491273 | |
| AIC | 3.228796 | 1.967890 | 0.891344 | 0.245776 | 0.102355 | 0.083123 | 0.071226 |
3.5 L-BPNN神经网络建模
4 结果与分析
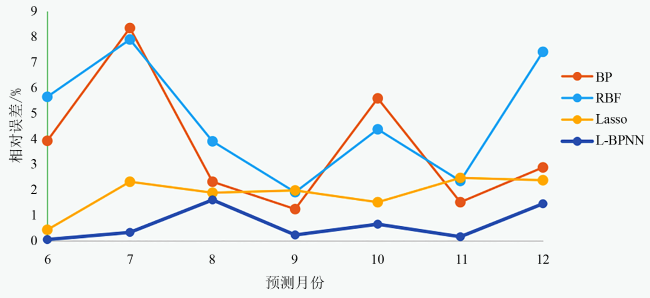
4.1 L-BPNN组合模型预测结果分析
表2 L-BPNN组合模型预测结果Table 2 Prediction results of L-BPNN combined model |
| 月份 | 真实值/CNY | 预测值/CNY | 绝对误差/CNY | 相对误差/% |
|---|---|---|---|---|
| 6 | 2.129618364 | 2.127834559 | -0.001783805 | 0.08 |
| 7 | 2.343750000 | 2.351965774 | 0.008215774 | 0.35 |
| 8 | 2.978162865 | 2.929674385 | -0.048488480 | 1.62 |
| 9 | 3.314072948 | 3.324556398 | 0.010483450 | 0.31 |
| 10 | 3.173002850 | 3.195643321 | 0.022640471 | 0.71 |
| 11 | 3.097538197 | 3.092345332 | -0.005192865 | 0.17 |
| 12 | 3.987193719 | 3.931245568 | -0.055948151 | 1.40 |