1 引 言
2 CFD风场建模
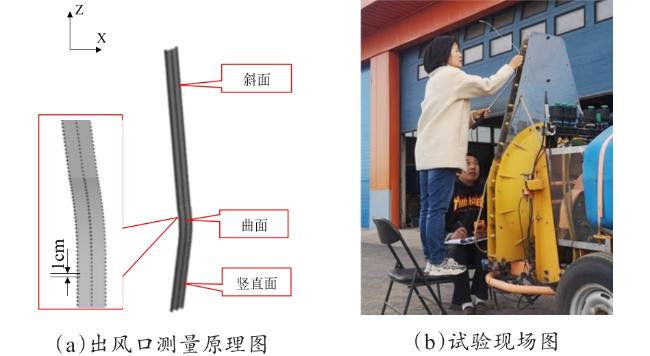
2.1 喷雾机结构
2.2 控制方程与建模方法
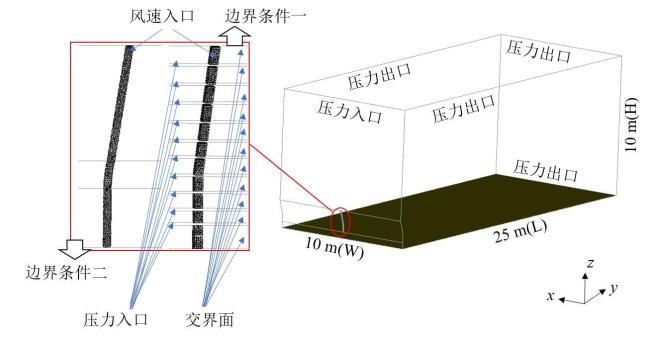
2.3 边界条件
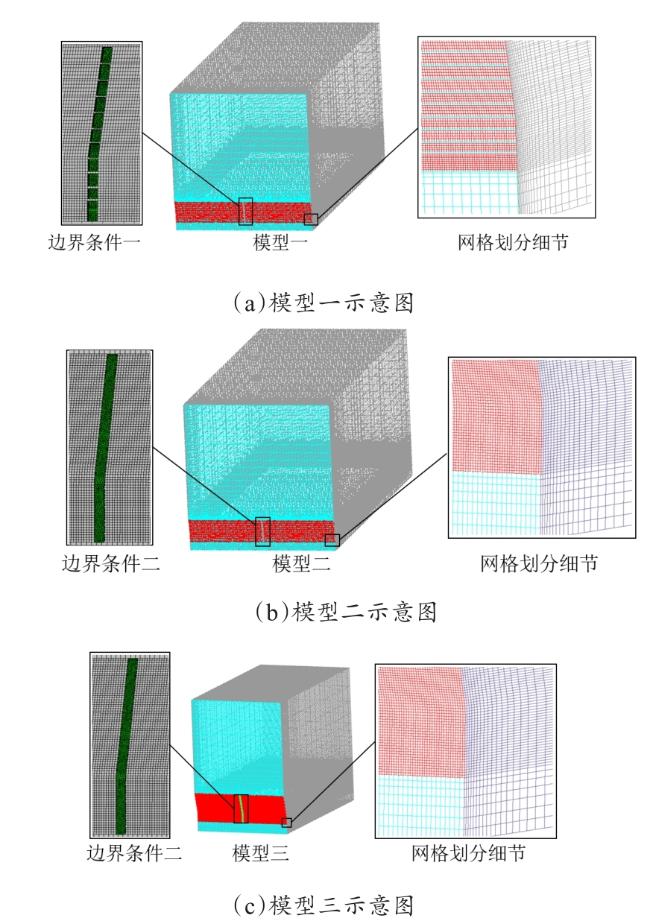
2.4 计算域与网格划分
表1 不同边界条件研究三种模型网格数量与尺寸Table 1 Grid parameters of three models |
| 网格数量与参数设置 | 模型一 | 模型二 | 模型三 |
|---|---|---|---|
| 四面体网格数量 四面体网格参数/m | 4201 0.02 | 4474 0.02 | 8242 0.01 |
| 正六面体网格数量 | 3,820,375 | 3,434,833 | 1,114,074 |
| 正六面体网格参数/m | 0.02 | 0.02 | 0.02 |
3 试验材料和方法
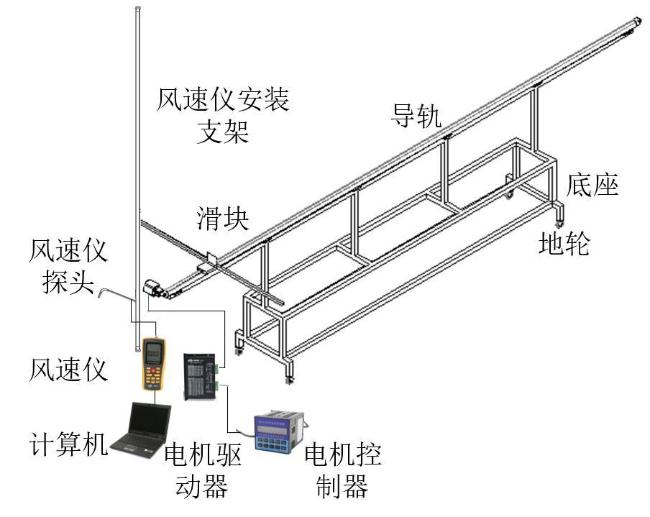
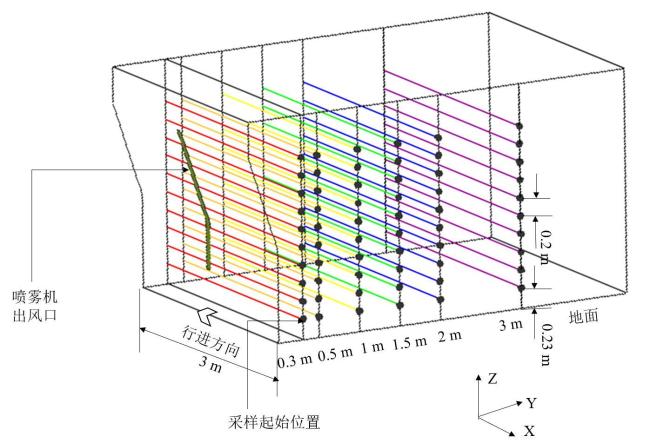
3.1 空间风场立体测量试验台设计
3.2 田间试验方法
4 仿真结果与验证
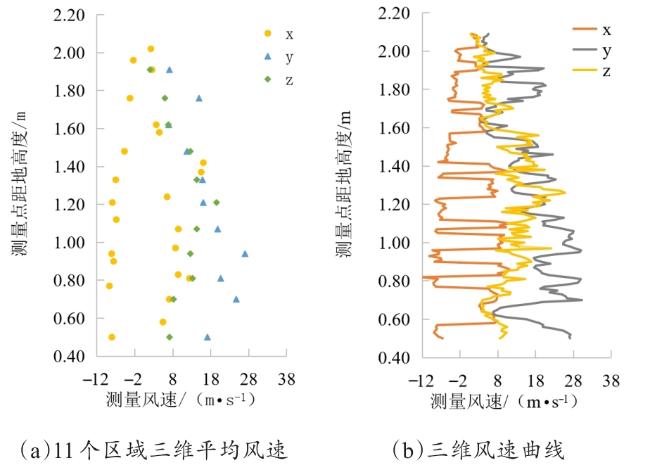
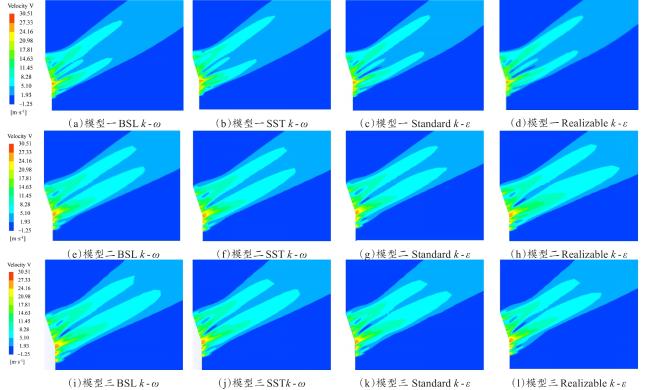
4.1 空间风场立体测量试验台设计
表2 不同湍流模型计算的3种CFD模型特性Table 2 Characteristics of three CFD models for different turbulence models |
| 特性 | 模型一 | 模型二 | 模型三 |
|---|---|---|---|
| 湍流模型 与连续性残差 | SST ,2.43×10-2 | SST ,2.70×10-3 | SST ,4.05×10-3 |
| BSL ,2.47×10-2 | BSL ,9.71×10-2 | BSL ,2.31×10-3 | |
| Standard ,5.30×10-2 | Standard ,k发散 | Standard ,4.54×10-2 | |
| Standard ,4.09×10-3 | Standard ,1.91×10-2 | Standard ,1.38×10-2 | |
| RNG ,3.30×10-1 | RNG ,1.88×10-1 | RNG ,9.12×10-2 | |
| Realizable ,3.99×10-3 | Realizable ,1.88×10-2 | Realizable ,2.76×10-2 | |
| 运算结果 是否可接受 | RNG 湍流模型,连续方程残差偏大,运算结果不可接受;其余湍流模型运算结果均可接受 | Standard 湍流模型,k发散,模型不收敛;RNG 湍流模型,连续方程残差不低于10-2;其余湍流模型运算可接受 | 对于六种湍流模型,运算结果均可接受 |
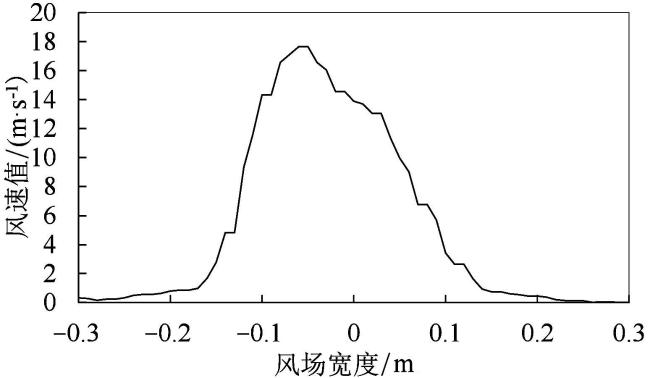
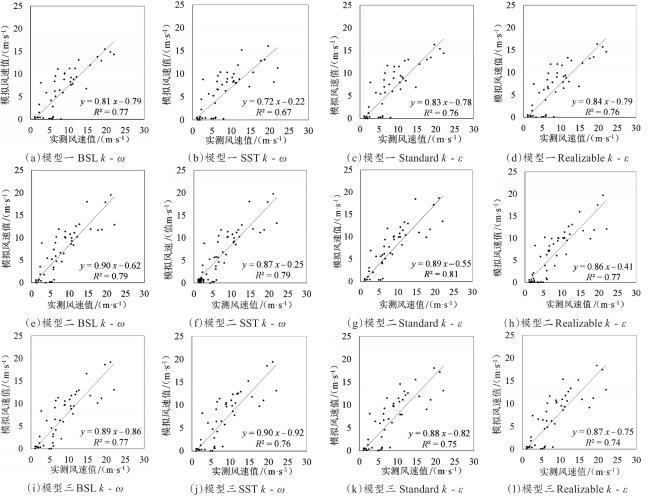
4.2 模型验证
表 3 喷雾风场不同高度和不同水平距离时风场宽度方向的实测最大风速 (m/s)Table 3 Peak measurement air velocity of sampling points with different height and horizontal distances |
| 水平距离/m | 距地高度/ m | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.23 | 0.43 | 0.63 | 0.83 | 1.03 | 1.23 | 1.43 | 1.63 | 1.83 | 2.03 | |
| 0.3 | 1.099 | 5.962 | 14.73 | 22.03 | 17.65 | 21.07 | 11.78 | 15.7 | 11.36 | 7.208 |
| 0.5 | 1.744 | 2.489 | 5.901 | 18.67 | 10.68 | 19.61 | 12.09 | 10.67 | 10.26 | 8.847 |
| 1.0 | 1.151 | 5.362 | 4.866 | 8.034 | 11.13 | 10.5 | 12.72 | 9.014 | 6.39 | 8.544 |
| 1.5 | 1.439 | 1.901 | 1.413 | 4.302 | 5.784 | 5.401 | 7.678 | 8.974 | 6.578 | 4.173 |
| 2.0 | 2.126 | 1.604 | 1.932 | 2.554 | 1.33 | 3.336 | 5.845 | 6.593 | 2.717 | 6.337 |
| 3.0 | 1.901 | 1.547 | 1.59 | 1.81 | 2.61 | 1.182 | 3.749 | 1.964 | 2.264 | 2.303 |