0 引 言
1 农机多机编队协同的控制策略设计
1.1 多机编队协同场景描述
图1 农机编队协同行驶初始状态示意图Fig. 1 Initial state schematic diagram of agricultural machinery convoy cooperative driving |
图2 农机编队协同行驶最终状态示意图Fig. 2 Final state schematic diagram of agricultural machinery convoy cooperative driving |
表1 农机编队初始状态参数Table 1 Initial state parameters of agricultural machinery in formation form |
| 参数符号 | 物理意义 | 数值 |
|---|---|---|
| 头车初始位置 | (50,6) | |
| 头车初速度/( ) | 12 | |
| 1号车初始位置 | (40,10) | |
| 1号车初速度/( ) | 14 | |
| 2号车初始位置 | (20,2) | |
| 2号车初速度/( ) | 16 | |
| 3号车初始位置 | (1,6) | |
| 3号车初速度/( ) | 15 |
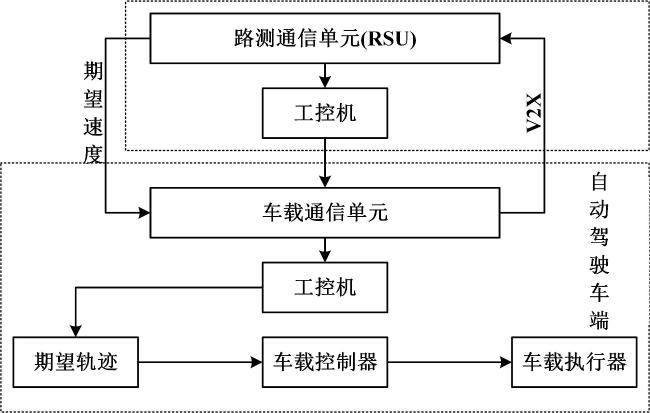
1.2 多机编队协同架构
1.2.1 车联网技术
1.2.2 架构设计
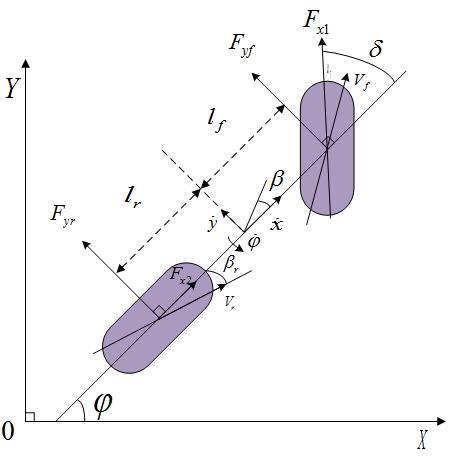
2 农机运动学和动力学模型建立
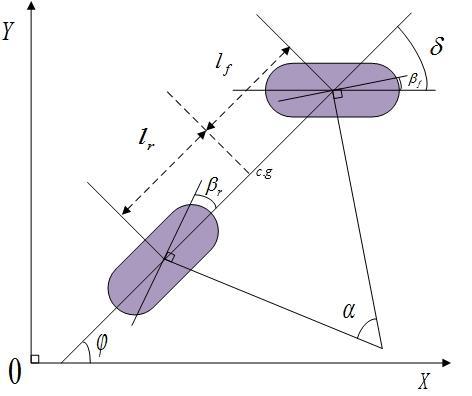
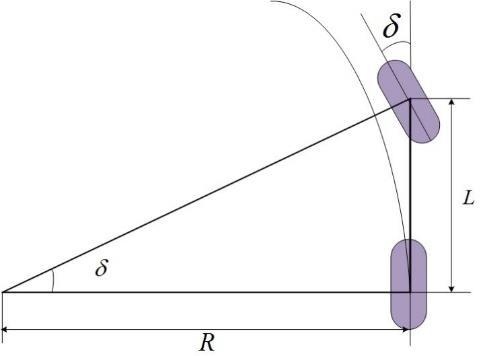
2.1 农机运动学模型
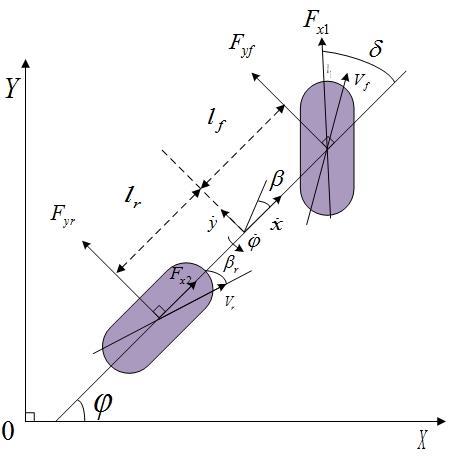
2.2 农机动力学模型
3 车辆编队控制器设计
3.1 线性调节跟踪器设计
3.2 延时补偿控制器设计
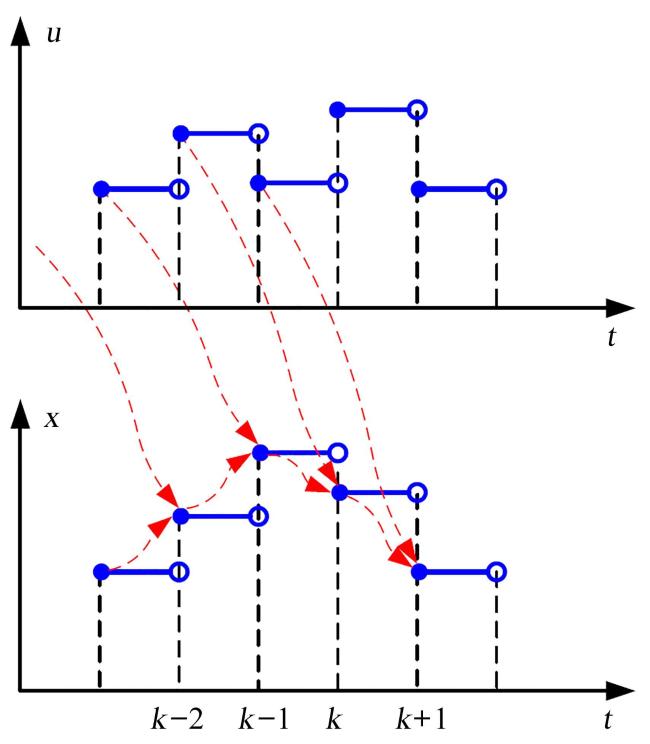
3.2.1 线性化与离散化
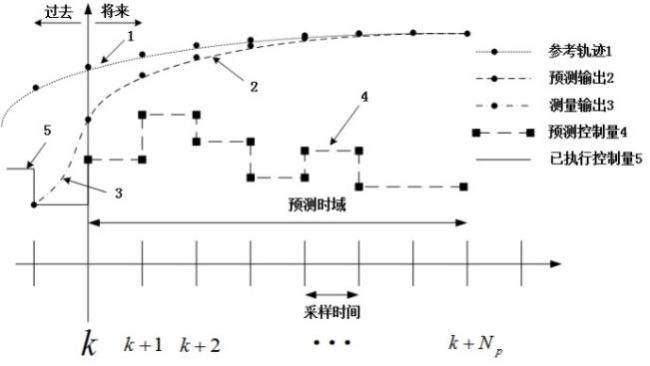
3.2.2 预测模型
3.2.3 目标函数
3.2.4 约束函数
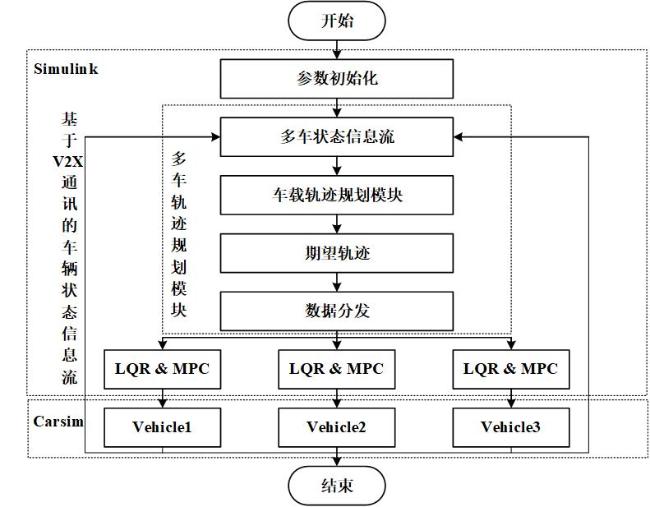
4 基于Carsim和Simulink的联合仿真实验
4.1 联合仿真平台搭建
表2 编队行驶农机单机动力学相关参数Table 2 Relevant parameters of single machine dynamics for formation running agricultural machinery |
| 参数符号 | 物理意义 | 数值 |
|---|---|---|
| 前轮侧偏刚度 | 61 135 N/rad | |
| 后轮侧偏刚度 | 61 135 N/rad | |
| 整车质量 | 1 465 kg | |
| 前轴距 | 1.2 m | |
| 后轴距 | 1.6 m |
4.2 控制器参数设置
4.2.1 速度变换器
4.2.2 离散行驶控制器
4.2.3 车辆动力机构
4.2.4 单车控制器参数设置
5 基于MPC延时补偿器轨迹跟踪仿真
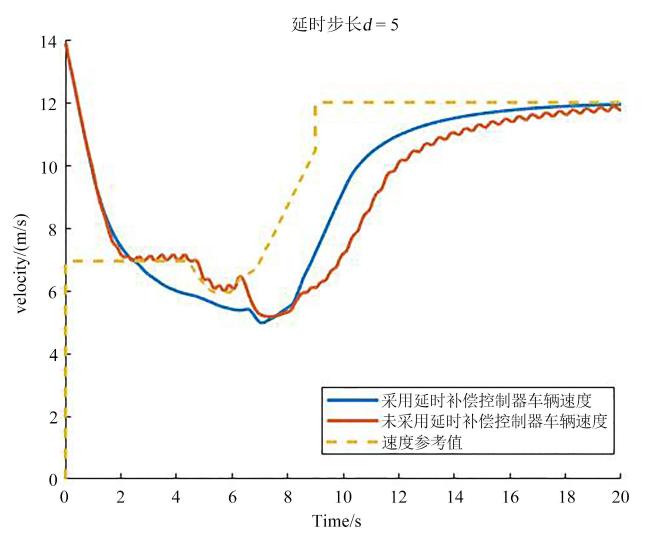
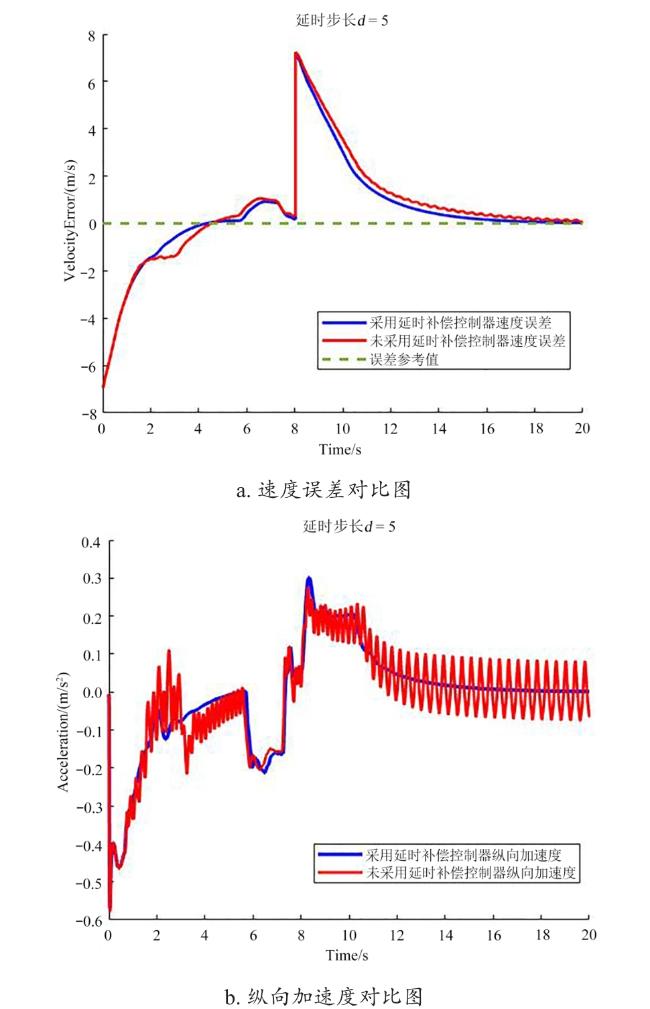
5.1 延时步长d=5
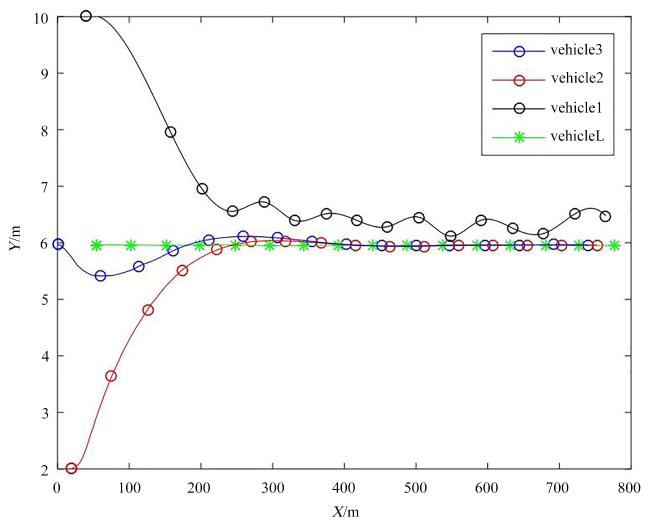
图13 1号车延时步长d =5四车轨迹曲线 Fig. 13 Trajectory curves of four vehicles with delay step length d=5 for Vehicle 1 |
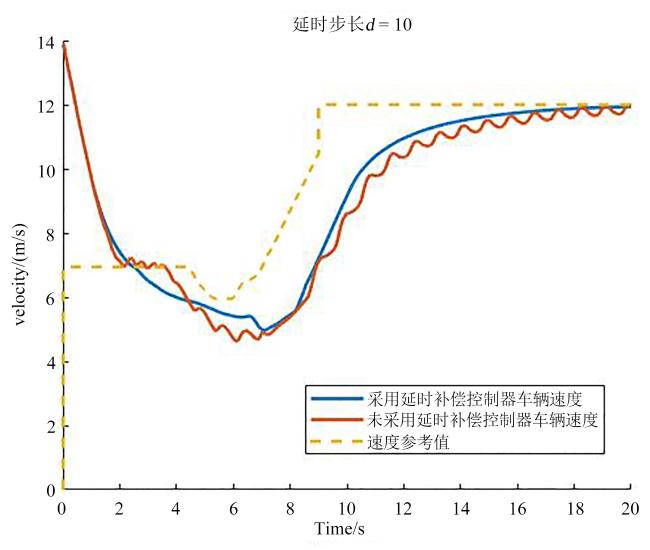
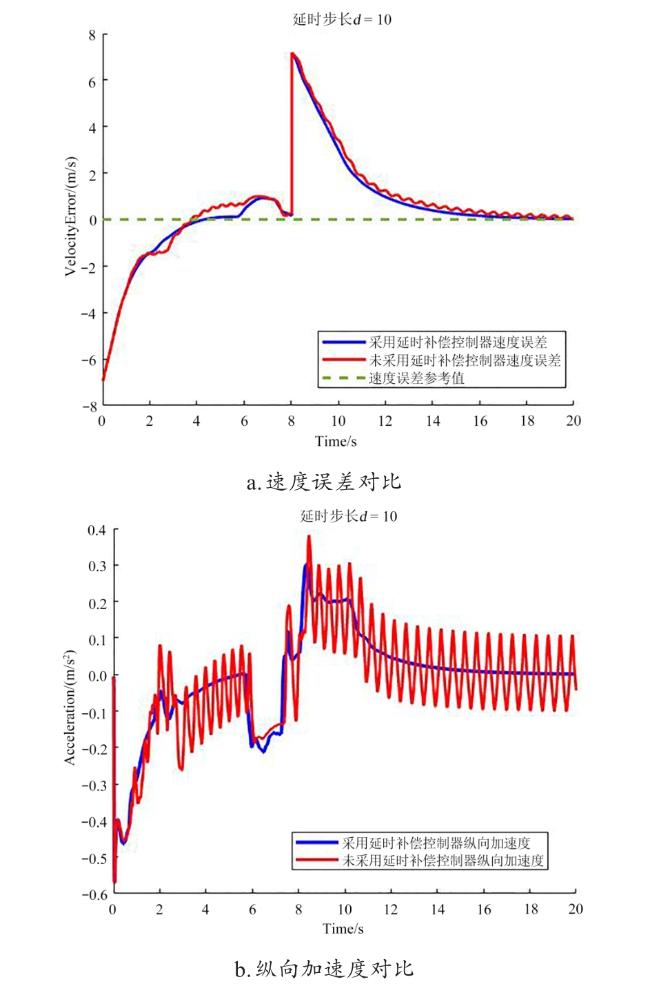
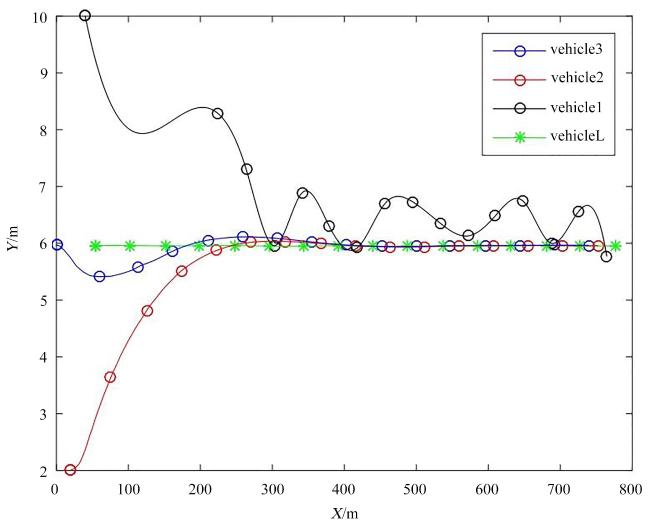
5.2 延时步长d=10
图17 带延时补偿4车轨迹曲线(d =5) Fig. 17 Trajectory curves of a four-vehicle convoy with delay compensation (d =5) |