0 引 言
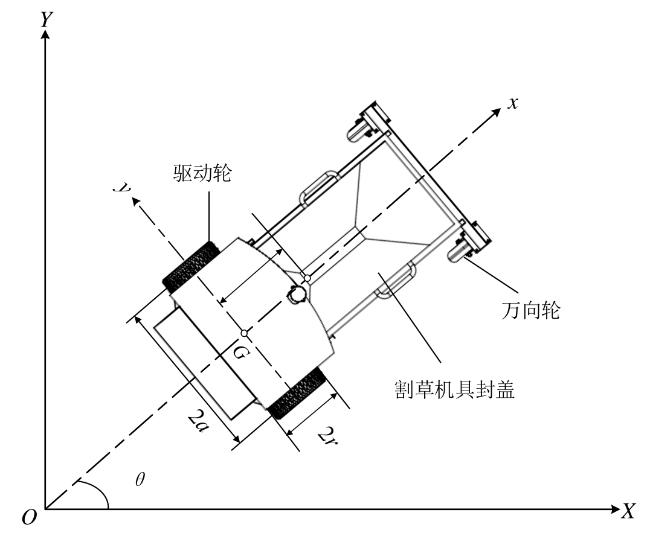
1 割草机器人建模
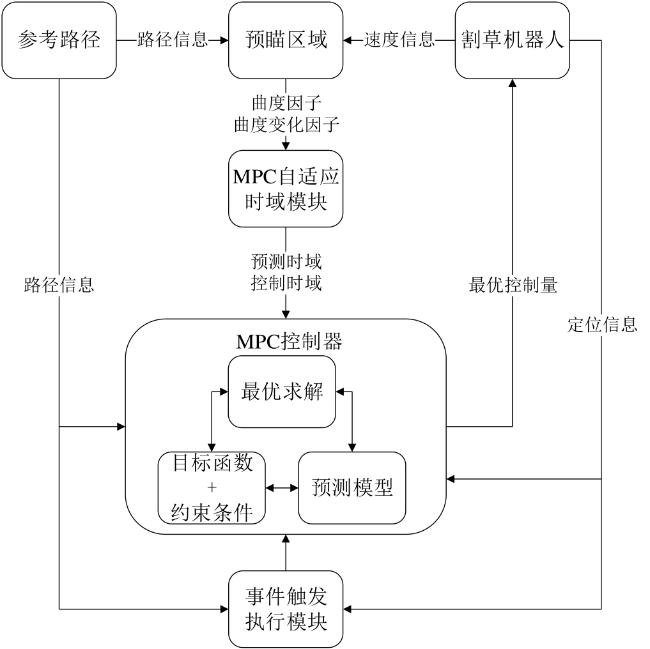
2 自适应时域模型预测控制器设计
2.1 MPC控制器设计
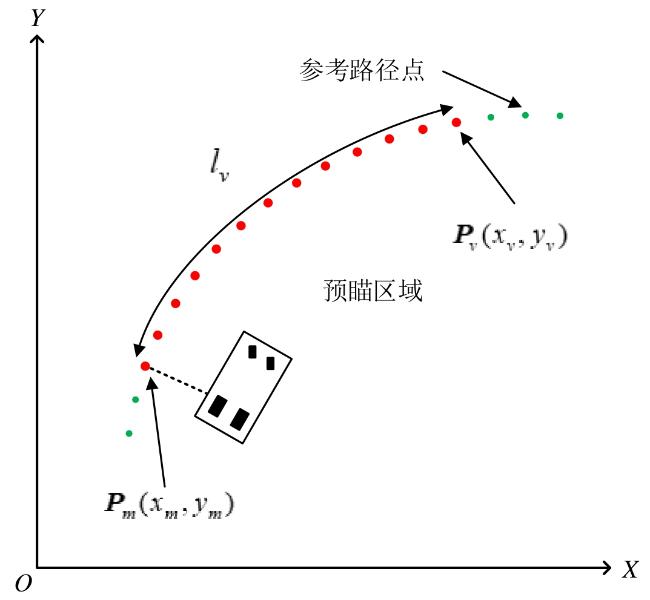
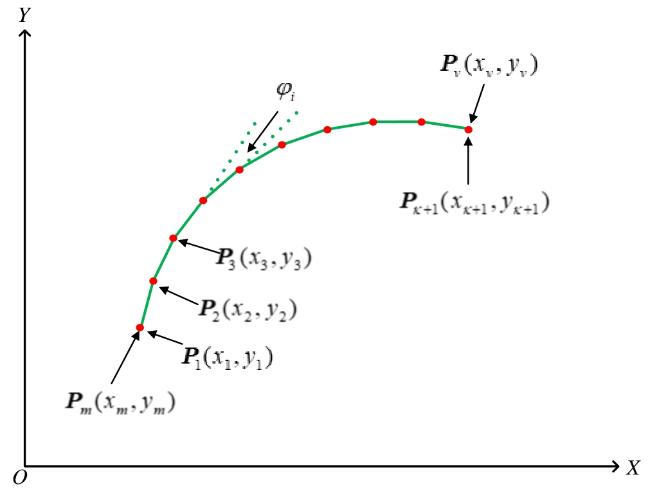
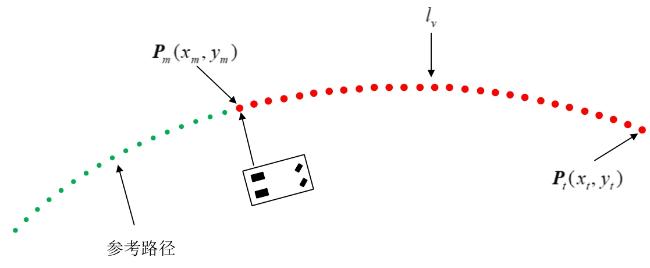
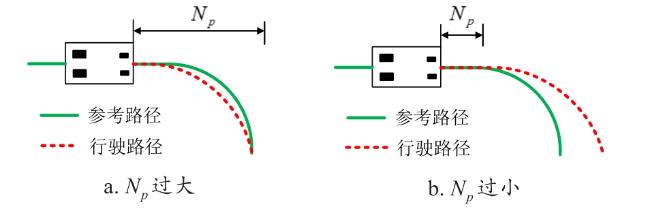
2.2 预瞄区域的确定
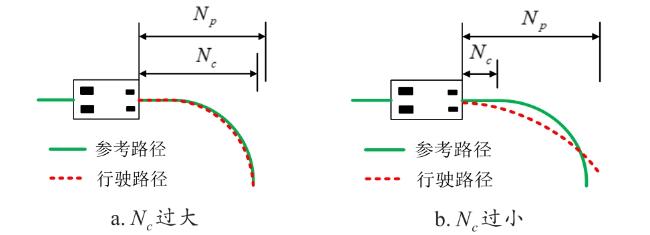
2.3 MPC自适应时域模块设计
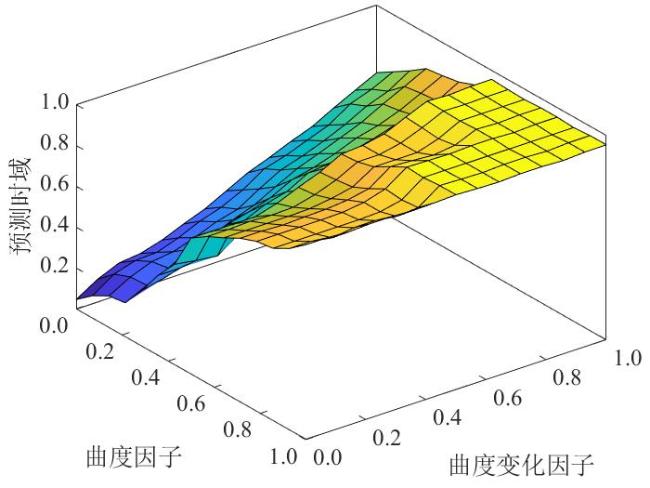
2.3.1 MPC自适应时域优化策略
2.3.2 模糊输入与模糊规则
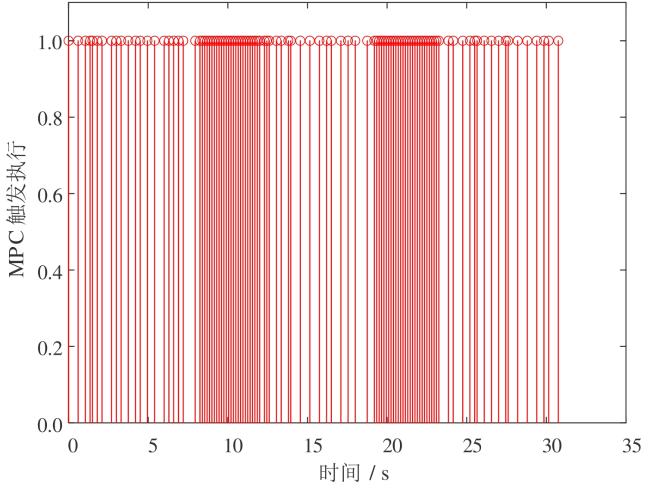
2.4 MPC事件触发执行模块设计
| 算法:MPC事件触发执行机制 |
|---|
| 1. 初始化:设置触发条件阈值:横向误差阈值 、航向误差阈值 、曲度因子阈值 、曲度变化因子阈值 。定义误差缓存队列: 、 2. while未到达参考路径终点 3. 将横向误差 和航向误差 分别存入缓存队列 、 4. if or 5. MPC求解最优控制序列 U (1:m× ),并将 U (1:m 6. else 7. 计算 、 8. if 第一次运行 9. MPC求解最优控制序列 U (1:m× ) 10. else 11. If or or size 12. MPC求解最优控制序列 U (1:m× ),清空误差缓存队列: 、 13. end if 14. end if 15. 将 U (1:m)作为控制输入 16. 将控制序列前m个移除得到 U 17. end if 18. end while |
3 试验验证
3.1 试验平台
3.2 试验设置
表3 割草机器人自适应时域MPC控制试验参数Table 3 Experimental parameters for adaptive time horizon MPC control of mowing robots |
| 参数 | 数值 |
|---|---|
| 采样周期 /s | 0.1 |
| 权重矩阵 | |
| 权重矩阵 | |
| 松弛因子最大值 | 1 |
| 松弛因子权重系数 | 10 |
| 最大线速度 /(m/s) | 2 |
| 最小线速度 /(m/s) | 0.3 |
| 预瞄区域最小长度 /m | 1.5 |
| 预瞄区域最大长度 /m | 5 |
| 时域权重系数 | 0.5 |
| 曲度变化增益系数 | 0.8 |
| 横向误差阈值 | 0.02 |
| 航向误差阈值 | 0.02 |
| 曲度因子阈值 | 0.5 |
| 曲度变化因子阈值 | 0.5 |
3.3 试验结果与分析
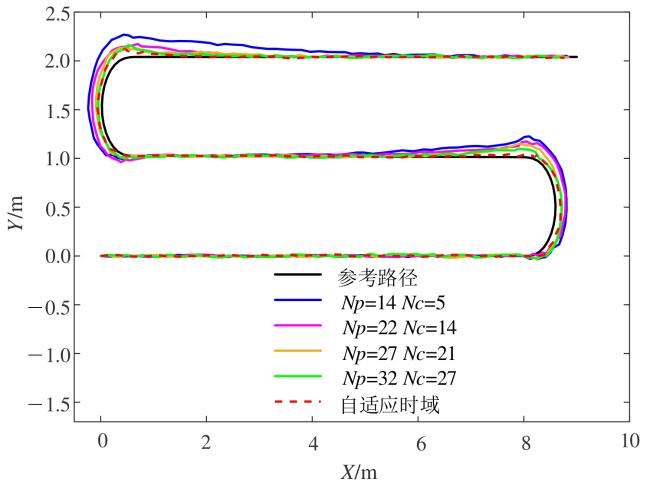
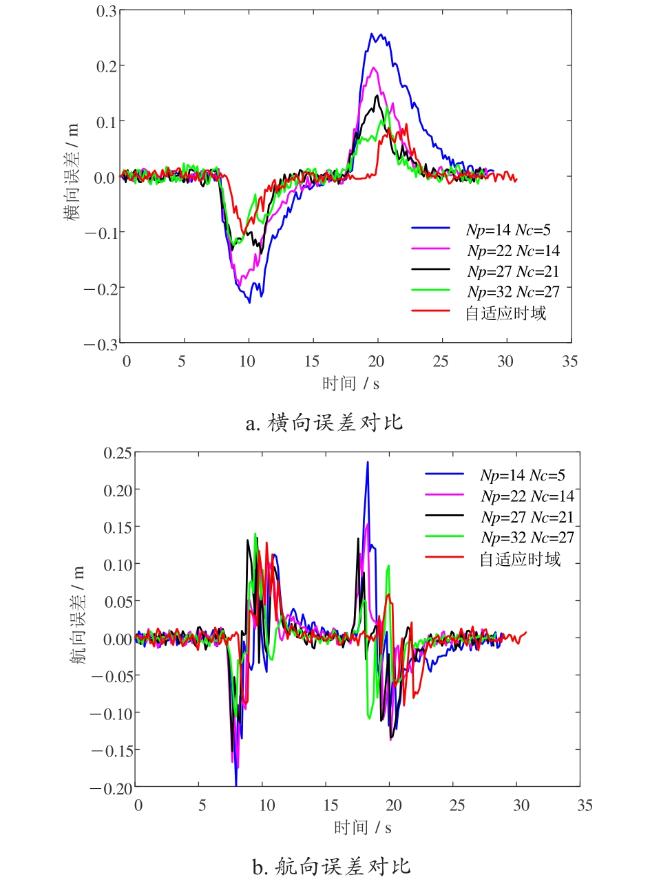
图15 割草机器人路径跟踪误差对比图Fig. 15 Comparison chart of path tracking errors for mowing robots |
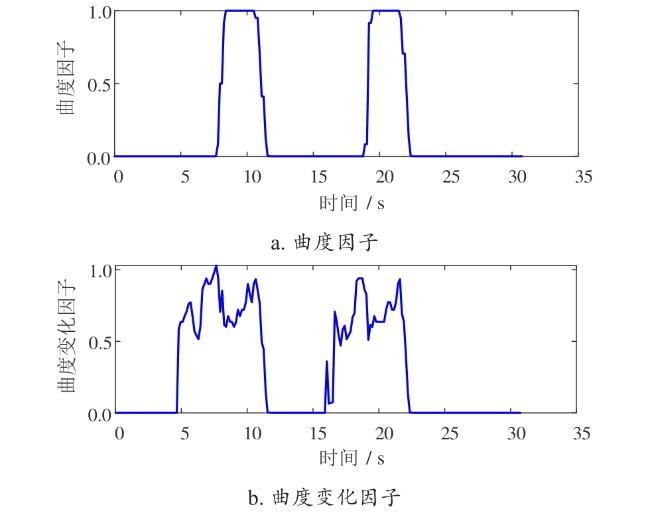
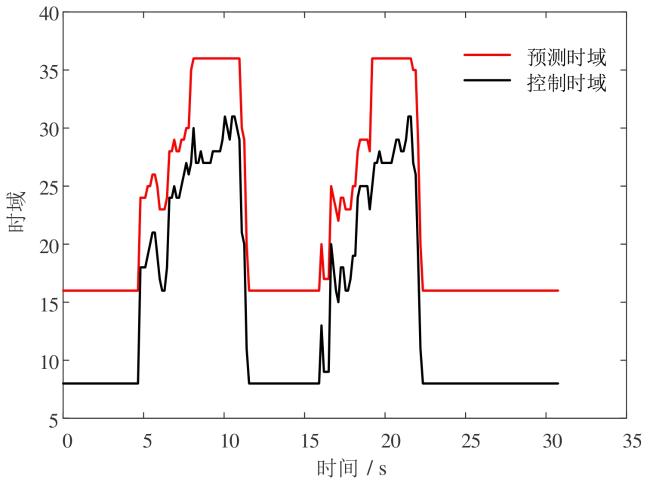
图16 预瞄区域的曲度因子及曲度变化因子Fig. 16 Curvature factor and curvature variation factor of the preview area |
表4 割草机器人试验固定时域与自适应时域MPC控制性能Table 4 MPC Control performance of fixed time horizon and adaptive time horizon in mowing robot experiment |
| MPC预测时域 | 第1组
| 第2组
| 第3组
| 第4组
| 自适应时域 |
|---|---|---|---|---|---|
| MPC控制时域 | |||||
| /m | 0.257 2 | 0.197 8 | 0.145 9 | 0.125 4 | 0.104 5 |
| /m | 0.071 1 | 0.046 5 | 0.032 7 | 0.028 4 | 0.017 5 |
| /m | 0.082 8 | 0.060 6 | 0.041 9 | 0.033 0 | 0.025 6 |
| /rad | 0.236 5 | 0.174 8 | 0.152 8 | 0.140 3 | 0.128 3 |
| /rad | 0.039 6 | 0.033 7 | 0.027 8 | 0.024 5 | 0.016 7 |
| /rad | 0.041 0 | 0.037 5 | 0.035 0 | 0.029 4 | 0.025 5 |
| /s | 0.006 7 | 0.010 3 | 0.012 6 | 0.015 8 | 0.004 9 |
图18 割草机器人路径跟踪中的参考路径曲率Fig. 18 Reference path curvature in mowing robots path tracking |