Welcome to Smart Agriculture 中文
Smart Agriculture

Smart Agriculture >

2020 , Vol. 2 >Issue 3: 129 - 138

DOI: https://doi.org/10.12133/j.smartag.2020.2.3.201912-SA004

Information Processing and Decision Making

Hyperspectral Estimation Model Construction and Accuracy Comparison of Soil Organic Matter Content

  • LIU Tianlin , 1 ,
  • ZHU Xicun , 1, 2 ,
  • BAI Xueyuan 1 ,
  • PENG Yufeng 1 ,
  • LI Meixuan 1 ,
  • TIAN Zhongyu 1 ,
  • JIANG Yuanmao 3 ,
  • YANG Guijun 4
Expand
  • 1. College of Resources and Environment, Shandong Agricultural University, Tai'an 271018, China
  • 2. National Key Laboratory for Efficient Utilization of Soil and Fertilizer Resources, Tai'an 271018, China
  • 3. College of Horticulture Science and Engineering, Shandong Agricultural University, Tai'an 271018, China
  • 4. National Engineering Research Center for Information Technology in Agriculture, Beijing 100097, China

Received date: 2019-12-23

  Revised date: 2020-06-26

  Online published: 2020-09-29

Fold

Highlights

Soil organic matter (SOM) is an important source of crop growth, its content can reflect soil fertility status. In order to realize the fast and real-time estimation of the SOM, based on hyperspectral data, a rapid estimation model of SOM content in orchards was established. A total of 100 brown soil samples were collected from the apple orchard of Qixia county, Yantai city, Shandong province. After drying and grinding, the hyper-spectrum of the soil was measured in the laboratory using ASD FieldSpec. The spectral data was preprocessed by the method of moving average, and the spectral reflectance features of orchard soil were analyzed to study the correlation between spectral reflectance and its soil organic matter content. In order to enhance the correlation between relevant spectral parameters and soil indexes, the original data were processed by using the multivariate scattering correction, the first derivative and the first derivative of MSC. After the sensitive wavelengths of soil organic matter content were selected and the spectral indexes were constructed. Multiple linear regression models (MLR), support vector machines (SVM) and random forest (RF) models were respectively established. The estimation accuracy of the orchard soil organic matter estimation model was measured by the determination coefficient (R 2), root mean square error (RMSE) and relative analysis error (RPD). The sensitive wavelengths of soil organic matter content selected were 678, 709, 1931, 1939, 1996 and 2201 nm. The spectral parameters were constructed using the selected wavelengths, which were NDSI(678, 709), NDSI(678, 1931), NDSI(678, 2201), NDSI(709, 1939), and NDSI(1939, 2201). These models established include MLR, SVM and RF model. The RF model had the best precision. The calibration sample R 2 was 0.8804, the RMSE was 0.1423 and RPD reached 2.25; the R 2 of the verification model was 0.7466, the RMSE was 0.1266, and the RPD was 1.79. The results showed that the fitting effect of the hyperspectral inversion model based on RF regression analysis was better than that based on MLR analysis and SVM regression analysis. As a promising and effective method, RF can play a vital role in predicting soil organic matter. The results can help understanding the distribution of soil nutrients, guiding farmers to apply fertilizer reasonably and improving the efficiency of orchard production and management.

Cite this article

LIU Tianlin , ZHU Xicun , BAI Xueyuan , PENG Yufeng , LI Meixuan , TIAN Zhongyu , JIANG Yuanmao , YANG Guijun . Hyperspectral Estimation Model Construction and Accuracy Comparison of Soil Organic Matter Content[J]. Smart Agriculture, 2020 , 2(3) : 129 -138 . DOI: 10.12133/j.smartag.2020.2.3.201912-SA004

1 引 言

土壤有机质（Soil Organic Matter，SOM）是作物生长的重要来源，其含量能够反映土壤肥力状况，对作物的生长发育有着显著影响［1］，是表征土地质量的重要指标之一［2］。然而土壤是一个综合复杂的生态系统，土壤养分含量指标的定量评价及其研究一直以来都是土壤学科的重点与难点。SOM含量可以直接通过地面调查和观测获取，但此方法存在周期长、时效性差、成本高等缺点，所能达到的空间尺度也有一定的局限性［3］。研究表明，土壤的反射光谱能够反映土壤的理化性质［4］，高光谱等光谱分析技术可为快速、实时估测土壤有机质含量提供有效手段。
高光谱数据主要具有光谱分辨率高、光谱范围广、波段连续、信息含量丰富等特点。国内外众多学者分别利用不同的高光谱数据对SOM含量反演进行了研究。包青岭等［5］利用小波变换和数学变换进行光谱数据预处理，利用灰色关联分析与随机森林算法（Random Forest，RF）对特征光谱进行分析，并建立多元线性预测模型，结果表明，基于机器学习分类方法结合小波分解的土壤光谱有机质含量监测，可以有效提高特征波段的分类预测精度。李冠稳等［6］结合偏最小二乘回归和RF建立SOM含量估算模型，并与竞争性自适应重加权算法、迭代保留有效信息变量、连续投影算法和遗传算法所得结果进行比较，挑选出建立RF模型的51个变量数，模型相对分析误差（Relative Percent Deviation，RPD）达到4.7，能够很好地预测SOM含量。George等［7］利用高分辨率高光谱卫星/机载数据，获取可见光区的敏感带产生各种光谱指数，通过神经网络模型和光谱敏感指数对SOM中的有机碳含量进行预测，决定系数R 2达到0.92。Wei等［8］经过预处理得到的10个光谱指标，利用岭回归、核岭回归、贝叶斯岭回归和AdaBoost算法建立了基于特征波段的SOM高光谱反演模型。检测SOM含量具有检测精度高、速度快的特点，对精准农业的快速发展具有重要意义。
但高光谱同时也具有波段数目多、数据量大、信息冗余和重叠的缺陷。因此在针对光谱数据质量的研究中，前人主要通过对原始数据的各种变换和增强处理，提高光谱数据的质量，从而进行相关参数的构建及模型的反演。沈兰芝等［9］采用多种预处理方法，包括去噪处理、数据变换及降维处理，最终利用支持向量回归法和偏最小二乘回归法建立了土壤有机质含量估测模型，结果表明合适的预处理即小波去噪和主成分分析（Principal Component Analysis，PCA）降维相结合可有效改善光谱数据质量。国佳欣等［10］对土壤光谱进行了包含分数阶微分在内的数学变换，筛选出显著的波段构建了偏最小回归模型和BP神经网络模型，结果表明1.5阶导数对红壤光谱数据的变换能够更好地突出与有机质相关的特征信息，有助于其含量预测，并且复合模型能够更好地预测SOM含量。
前人研究中除了对数据进行各种增强光谱信息、提高数据质量的预处理外，还针对经过预处理的光谱构建了多种光谱参数，用以反演SOM含量。张智韬等［11］利用经过分数阶微分处理的光谱构建了归一化光谱指数，经过筛选获得敏感指数后构建RF模型，结果对不同类别土质均有较好的评估效果。除了最常见的数学方法，新的处理技术也用于处理光谱数据。王延仓等［12］采用二进制小波技术将土壤光谱数据分离为5个尺度的高频数据与低频数据，再将低频数据、高频数据分别与土壤有机质实测数据进行相关性分析，提取最佳波段组合，构建有机质含量诊断模型，结果表明，与数学方法相比，基于二进制小波变换算法构建的模型精度较高，稳定性较好，其最优模型的预测精度提高了31.5%。
前人研究表明，针对高光谱数据的特点，无论是算法构建还是数据处理方法选取，均是为了解决高光谱数据的冗余和重叠现象，最终改善光谱数据质量，提高模型反演精度。有机质含量是衡量土壤肥力的重要指标，对农产品的产量和品质起到关键作用。由于研究区果园位于丘陵地区，不同的果园由于土质（砂土/淤土/混合土）以及管理水平的不同，导致SOM含量也存在差异。本研究以果园土壤为研究对象，利用移动平均法对高光谱数据进行预处理，利用多元散射校正、MSC的一阶导数和一阶导数增强相关光谱参数与土壤指标的相关性。通过获得SOM含量的敏感波长，构建新的土壤归一化光谱指数，最后建立多元线性回归模型（Multiple Linear Regression，MLR）、支持向量机（Support Vector Machine，SVM）、RF三种估测模型，利用决定系数R 2和均方根误差RMSE、相对分析误差RPD来估算精度。为高光谱遥感在果园SOM含量估测中应用提供支持。

2 材料与方法

2.1　研究区概况

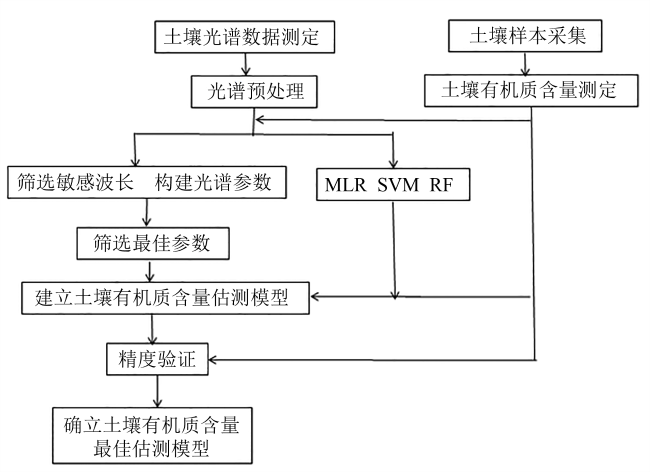
研究区位于山东省烟台市栖霞市（37°05′~37°32′N，120°33′~121°15′E），地处丘陵山区，土壤多属于棕壤土［13］。该地区气候为暖温带季风型半湿润气候，年平均气温11.4 ℃，年平均日照总时数为2659.9 h，平均地面温度13.6 ℃，年平均降水量为640~846 mm。

2.2　研究技术方法

本研究的技术流程如图1所示。通过采集获取不同果园的土壤样本测定其有机质含量以及高光谱反射率，利用光谱参数构建SOM含量反演模型，并进行模型精度验证。
图1 技术路线

Fig. 1 Technical route of the research

2.2.1　土壤样本的采集与处理

采样时间：2013年5月13日。
采样地点：栖霞市3个街道和12个乡镇中的25个苹果果园。
采样方法：每个果园中随机选取4棵苹果树，利用土钻在选择的每棵果树的树冠外沿垂直正下方的东西南北4个方位分别采集土壤，采样的深度为0~20 cm。将采集到的土壤充分混合均匀，每200 g作为1个样本，并对每个样本进行编号，共采集100个土壤样本。
将采集好的土壤样本中的植物根、残茬等杂质去除，在实验室内阴干，然后将土壤磨细、过筛、混合均匀。每个土壤样本采用四分法取样100 g盛于广口瓶中，采用重铬酸钾容量法-外加热法［14］进行土壤有机质的测定。把100个土壤样本有机质浓度梯度排列，采用等距抽样方法每隔3个选取1个样本，共取25个土壤样本用作模型验证，剩下的75个土壤样本用于建立估测模型。

2.2.2　土壤光谱测定

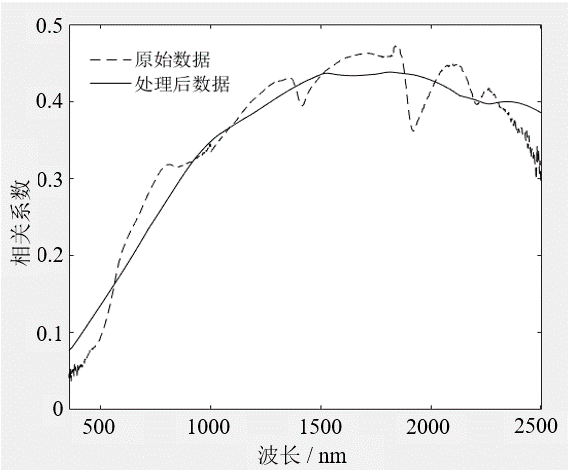
利用美国ASD FieldSpec3便携式地物光谱仪对土壤样本进行光谱测定，该仪器波段范围是350~2500 nm。在350~1000 nm范围之间，光谱采样间隔为1.4 nm，分辨率为3 nm；在1000~2500 nm之间光谱采样间隔为2 nm，光谱分辨率为10 nm。重采样间隔为1 nm，共输出2151个波段。土壤样本光谱测定在暗室环境下进行，将处理好的土壤样本装到直径15 cm、深2 cm的器皿中，装满后将土面刮平。采用50 W功率的卤素灯为光源，光源距离土样中心30 cm，距离土壤表面15 cm［15］。将光纤探头固定于三脚架上，探头视场角25°，光源入射角45°。在测定过程中转动器皿3次，每次转动90°，共测得四次数据后取平均得到该土样反射光谱数据［16］。

2.2.3　光谱数据预处理

在光谱数据采集过程中，由于外界环境条件的影响和地物波谱仪不同波段对能量响应的差异，获得的光谱存在噪声。为保证相关分析和后期的模型建立与检验的准确性，需对光谱数据进行预处理和数学变换。研究发现，当噪声频率较高时，采用移动平均法具有一定的去噪作用［17］，因此本研究采用移动平均法在MATLAB软件中对光谱数据曲线进行平滑处理，图2为随机选取的某条光谱曲线平滑处理对比图。
图2 光谱曲线平滑处理对比图

Fig. 2 Comparison chart of spectral curve smoothing process

为增强相关光谱参数与土壤指标的相关性，本研究采用多元散射校正（Multiple Scatter Correction，MSC）、一阶微分以及MSC的一阶微分对原始数据进行处理。MSC是现阶段多波长定标建模常用的一种数据处理方法，经过处理后的光谱数据可以有效地消除散射影响，增强光谱信息质量，相关公式如下。
计算平均光谱：
A ¯ = ∑ j = 1 M A j M
一元线性回归：
A j = m j A ¯ + b j
利用回归系数计算MSC校正后的光谱：
A j ( M S C ) = ( A j - b j ) m j
其中， A ¯  表示n×p维定标光谱数据矩阵；n为定标样品数；p为光谱采集所用的波长点数； A j（j=1，2，…，M）为移动平均处理后的光谱数据； m j和 b j是回归系数； A j ( M S C )为经MSC校正后的光谱数据。
一阶微分公式如下：
f ' ( X i ) = f X i + 1 - f ( X i - 1 ) / 2 ∆ λ
其中， f X i为各波段波长反射率； f ' ( X i )为波长 X i的一阶微分光谱； ∆ λ是波长Xi +1到 X i - 1的间隔。
经过预处理后的光谱数据与SOM含量进行相关性分析后，筛选出相关性系数较高的敏感波长。

2.2.4　土壤光谱指数计算

土壤高光谱波段数据众多，光谱数据变量之间存在较为严重的多重共线性，影响模型复杂结构。研究表明，通过构建归一化光谱指数（Normalized Difference Soil Index，NDSI）可以有效去除冗余信息变量，放大光谱特征信息［18］。本研究利用光谱预处理筛选出的敏感波长用于土壤光谱指数的构建，采用的 N D S I i , j公式如下。
N D S I ( i , j ) = ( R i - R j ) / ( R i + R j )
其中， R i和 R j分别为波长i和j的反射率，i和j的范围均在350~2500 nm间，且i＞j。

2.2.5　模型精度验证

本研究SOM估算模型的估算精度用R 2和RMSE、RPD（检验样本标准差SD与预测RMSE的比值）来衡量。对反演模型进行验证，若R 2越大，RMSE越小，则模型的精度越高，模型越稳定；反之，模型越不稳定［19］。另外，当RPD≥2时表明模型具有极好的预测能力，当1.4≤RPD＜2时表明模型可对样品作粗略估测，而RPD＜1.4则表明模型无法对样品进行预测［20］。

3 结果与分析

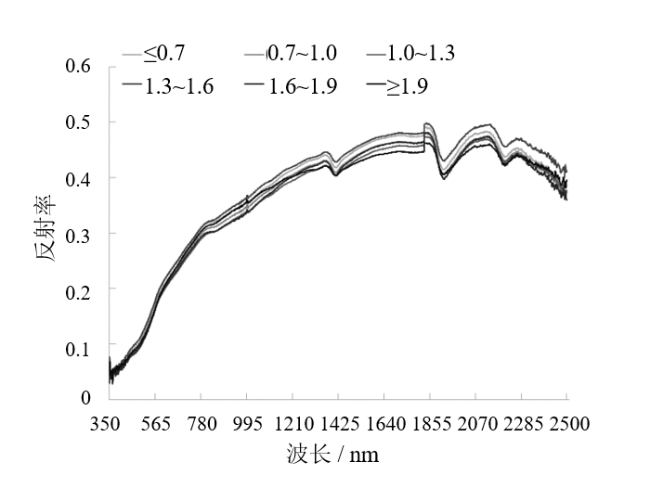
3.1　土壤有机质高光谱特征分析

对采集的果园土壤光谱数据进行分析。将SOM含量高低划分为6个等级，并且计算每个等级的光谱平均值，得到土壤SOM平均光谱曲线（如图3），表明不同等级SOM的土壤光谱反射率曲线变化趋势相近，且随着SOM的增加，反射率降低。其中在可见光范围内，各等级的土壤反射率随波长的增大而增大，且反射率受SOM含量的影响降低，不同等级的光谱曲线基本重合；在780 nm后各等级的曲线出现较明显分离，并且在红外波段范围内，较高SOM含量的土壤光谱反射率低于较低SOM含量的反射率。其中在1310、1700以及2120 nm附近的反射峰，在1405以及1920 nm附近的吸收谷，反射率高低与SOM含量高低也表现出负相关的趋势，即SOM增高，反射率值降低。2100 nm之后出现的峰谷主要是由残余在土壤中的少量水分以及空气中水吸收引起的［21］，该处的SOM高低对反射率的影响减弱。
图 3 果园土壤有机质含量的土壤反射光谱特征

Fig. 3 Soil reflectance spectrum characteristics of the orchard soil sample

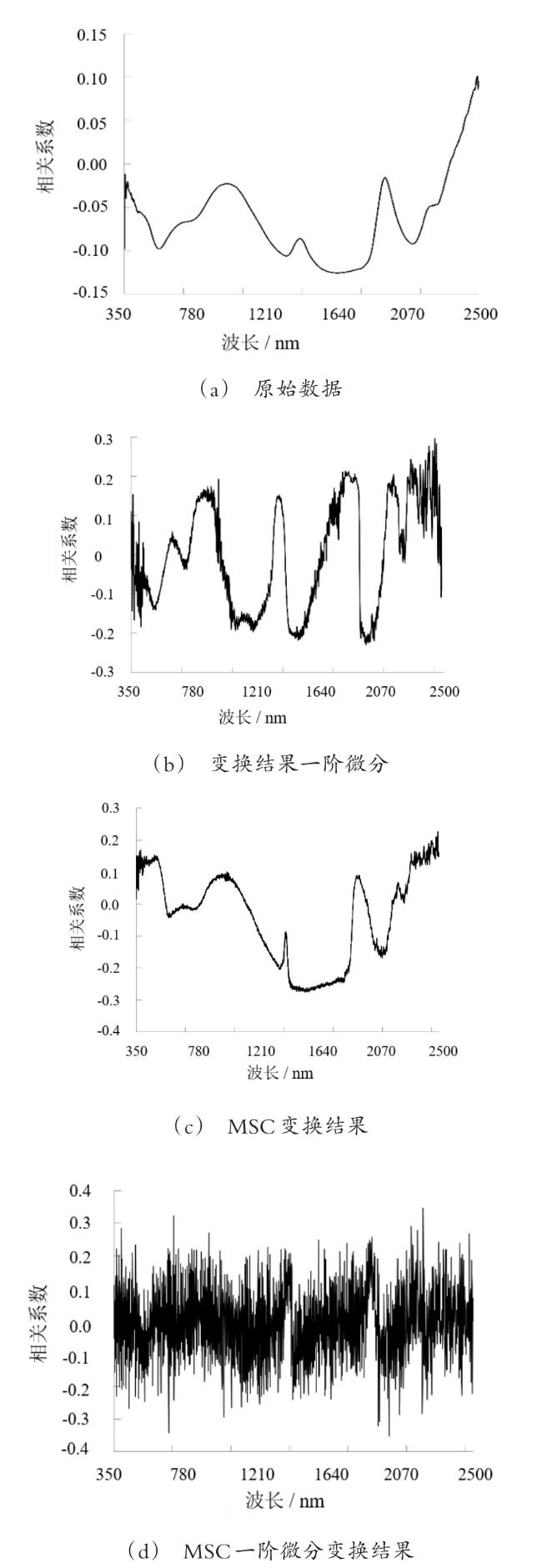
3.2　土壤有机质含量与高光谱数据的相关分析

为突出光谱曲线的反射和吸收特征，对原始光谱采用移动平均法预处理后所得到的光谱反射率数据进行原始数据一阶微分变换、MSC以及MSC一阶微分三种变换后，利用Excel对光谱数据与SOM含量分别进行相关性分析，结果如图4所示。
图4 SOM含量与高光谱反射率的相关系数

Fig. 4 Correlation coefficient of hyperspectral reflectance and SOM

原始光谱反射率与土壤有机质的含量相关性分析结果如图4（a）所示。从图中可以看出，原始土壤光谱反射率与有机质含量的相关系数小于0.1，并且整条曲线比较平滑，很难选出与有机质含量具有良好相关性的敏感波长。
通过对比可以看出，原始数据经过一阶微分变换和MSC处理后（图4（b）和图4（c）），虽然相关性有所提高但相关系数仍小于0.3，精度低。而MSC一阶微分的变换（图4（d））较好地提高了相关性，相关系数达到0.37。以上可以看出，不同的光谱变换方式，对应的相关性变化明显的波长也不同。同时，MSC变换方式能够在保留原始光谱相关性的基础上进行相关性的提高；而一阶微分变换方式虽然改变了原始数据相关性的变化趋势，但是能显著提高某些特定位置光谱的相关性，有利于光谱信息的挖掘。
根据以上分析结果，本研究最终采用MSC一阶微分的变换形式根据各波长反射率与SOM含量的相关性，按照从高到低最终筛选土壤有机质的敏感波长为678、709、1931、1939、1996和2201 nm。用筛选出的6个波长构建光谱参数与SOM进行相关性分析后选出相关系数较高的光谱参数。如表1所示。
表1 光谱参数与SOM相关系数

Table 1 Correlation coefficient between spectral parameters and SOM

光谱参数

相关

系数

 光谱参数

相关

系数

 光谱参数

相关

系数
NDSI(678, 709) -0.4685 NDSI(709, 1931) 0.3472 NDSI(1931, 1996) 0.3279
NDSI(678, 1931) 0.4317 NDSI(709, 1939) 0.4686 NDSI(1931, 2201) -0.4058
NDSI(678, 1939) 0.0395 NDSI(709, 1996) -0.4133 NDSI(1939, 1996) 0.0635
NDSI(678, 1996) 0.0046 NDSI(709, 2201) 0.2411 NDSI(1939, 2201) 0.5178
NDSI(678, 2201) -0.4307 NDSI(1931, 1939) 0.0193 NDSI(1996, 2201) -0.4104
根据表1结果进行筛选，通过对所有光谱参数与SOM含量相关系数的对比发现，相关系数较高的参数达到8个，包括NDSI（1939，2201）等，均达到0.4以上。为方便后续建模，按照相关系数由高到低最终选取的光谱指数为NDSI(678,709)、NDSI(678, 1931)、NDSI(678,2201)、NDSI(709,1939)和NDSI(1939,2201)。

3.3　土壤有机质含量估测模型的建立与检验

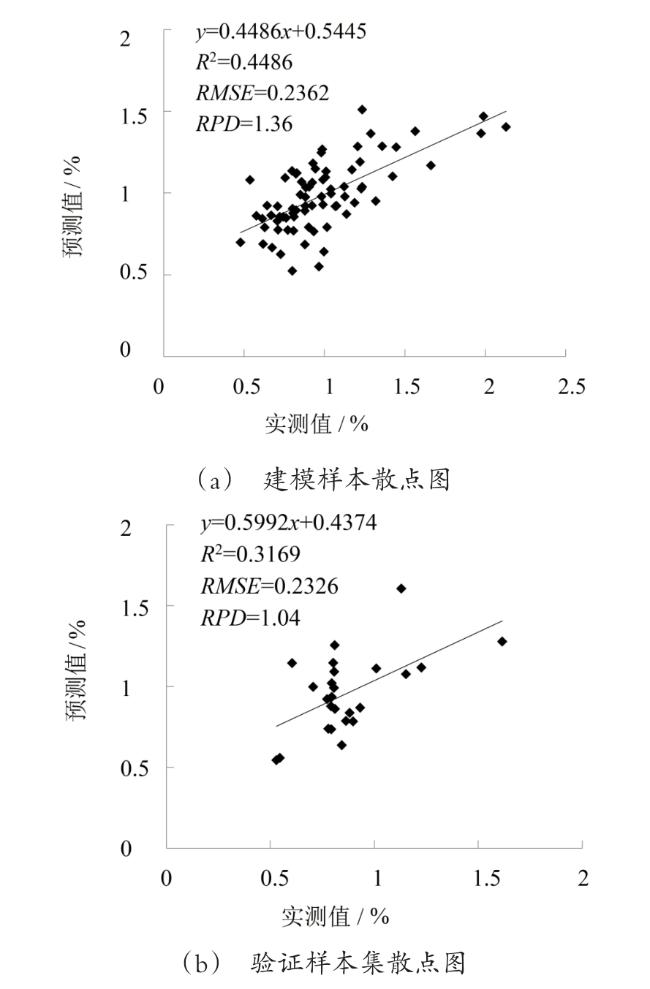
采用两种类型函数进行SOM估测模型的构建，一种是线性模型MLR，另一种是以非线性模型为核心的数据挖掘技术，包括SVM和RF。

3.3.1　MLR估测模型构建与检验

选取筛选出的敏感波长以光谱指数NDSI(678,709)、NDSI(678,1931)、NDSI(678,2201)、NDSI(709,1939)和NDSI(1939,2201)为自变量，建立MLR模型方程为：
y = 0.87004 + 142.8575 × X 1 + 268.9404 × X 2 + 184.2221 × X 3 + 32.4886 × X 4 + 76.2964 × X 5
其中，y为SOM估测含量；X 1~X 5为筛选的光谱指数。
MLR模型建模样本的拟合结果和验证样本集的预测结果如图5所示，从图5（a）看出建模样本的R 2为0.4486，RMSE为0.2362，RPD为1.36；图5（b）验证样本集的R 2为0.3169，RMSE为0.2326，RPD为1.04。多元线性回归模型R 2和RPD均较低，无法对样本进行预测。
图5 土壤有机质MLR模型检验

Fig. 5 MLR model test of SOM

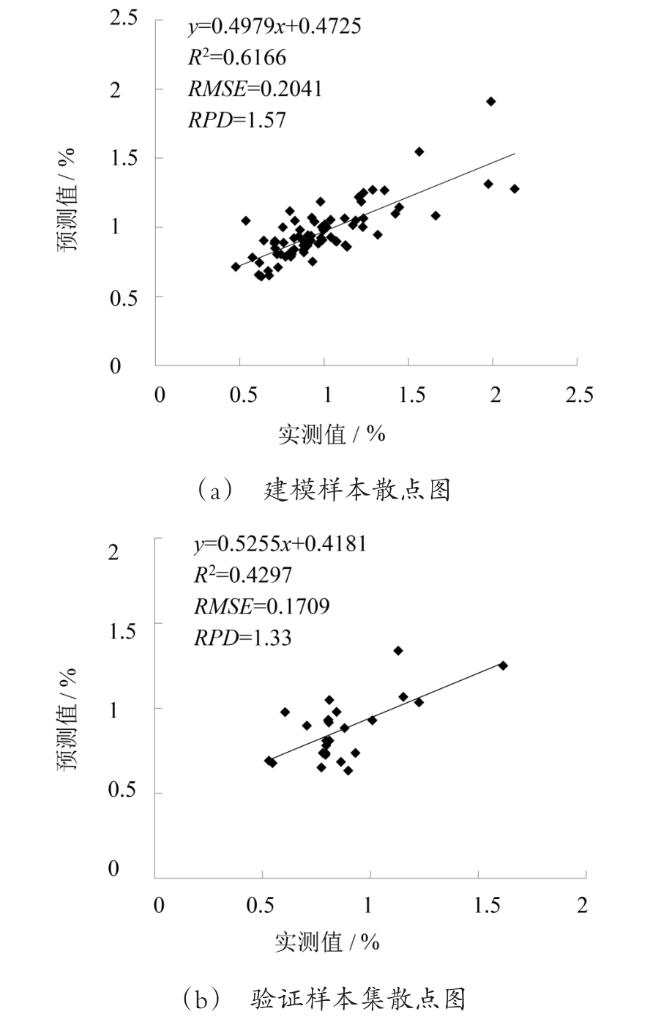
3.3.2　SVM估测模型建立与检验

将光谱指数NDSI(678,709)、NDSI(678,1931)、NDSI(678,2201)、NDSI(709,1939)、NDSI(1939,2201)作为自变量，SOM含量作为因变量，建立SVM模型。利用DPS进行SVM回归的运算，SVM类型是ε-支持向量回归（ε-Support Vector Regression，ε-SVR），核函数类型选择径向基函数（Radical Basis Function，RBF）。具体参数如表2所示。
表2 SVM回归模型参数

Table 2 SVM regression model parameters

Degree Gamma Coef0 Nu Epsilon Cashesize Cost Shrinking Prob P
3 1 0.001 0.5 0.001 100 1 1 1 0.01
SVM模型建模样本的拟合结果和验证样本集的预测结果图6所示，图6（a）为利用SVM回归法对建模样本处理得到的模型，R 2为0.6166，RMSE为0.2041，RPD为1.57；图6（b）为验证样本的R 2为0.4297，RMSE为0.1709，RPD为1.33。SVM的R 2和RPD值一般，只能够粗略地对样本进行预测。
图6 土壤有机质SVM回归模型检验

Fig. 6 SVM regression model test of SOM

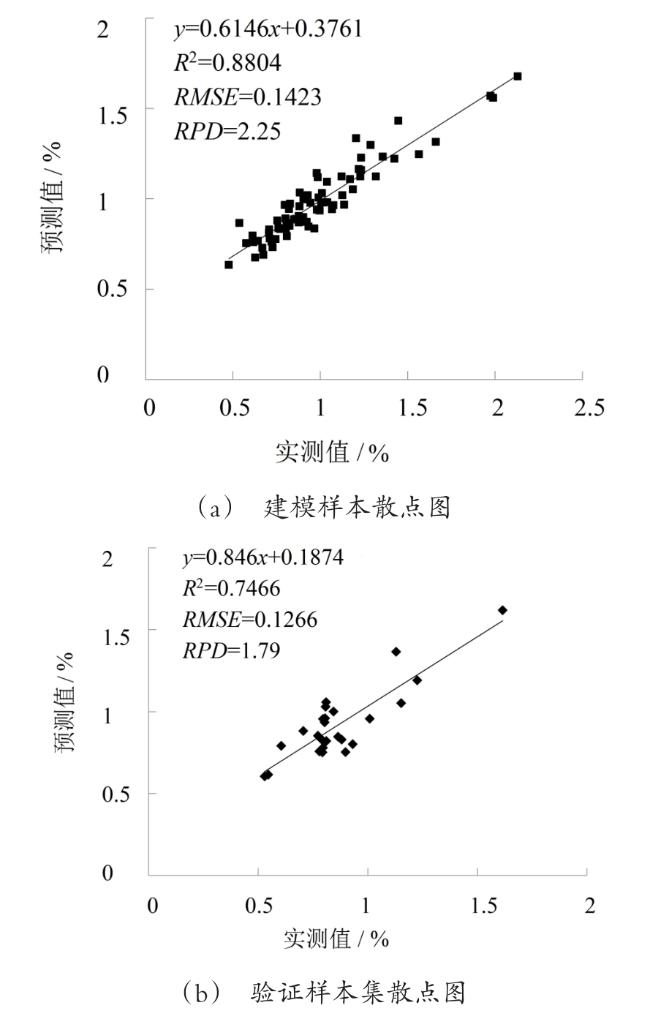
3.3.3　RF估测模型建立与检验

以光谱指数NDSI(678,709)、NDSI(678,1931)、NDSI(678,2201)、NDSI(709,1939)和NDSI(1939,2201)为估测模型的自变量，建立RF回归模型。RF回归模型建模样本的拟合结果和验证样本集的预测结果如图7所示，图7（a）中建模样本集的R 2为0.8804，RMSE为0.1423，RPD达到了2.25；图7（b）中验证模型的R 2为0.7466，RMSE为0.1266，RPD为1.79。结果表明RF的R 2和RPD值较好，可以有效地对样本进行预测，具有较好预测能力。
图7 土壤有机质RF回归模型检验

Fig. 7 RF regression model test of SOM

3.4　估测模型的对比分析

检验样本的各模型精度对比结果如表3所示，可以看出，RF回归模型的R 2最高且RPD＞2，说明具有较好的预测能力。而MLR模型R 2较低且RPD＜1.4，表明模型无法对样品进行预测。SVM回归模型的R 2处于中间位置，其RPD在1.4~2之间，表明模型可对样品作粗略估测。
表3 三种估测模型对比

Table 3 Comparison of three estimation models

建模方法 R 2 RMSE RPD
MLR 0.4486 0.2362 1.36
SVM 0.6166 0.2041 1.57
RF 0.8804 0.1423 2.25
因为RF回归模型的校正样本集的R 2为0.8804，RMSE为0.1423，RPD达到了2.25，基于RF回归分析建立的SOM的高光谱反演模型的拟合效果要优于MLR分析和SVM回归分析建立的高光谱反演模型，说明RF模型能够相对较好地估测SOM含量。

4 结 论

果园的SOM含量与果园的管理水平具有较大的关系，因此果园的施肥量、施肥种类、施肥方式以及果树的树龄树势等均会影响到果园土壤的有机质水平，并且体现在果树的基础产量上。本研究以山东省烟台栖霞市苹果果园土壤为研究对象，进行了SOM含量高光谱估测模型构建及精度对比研究，得出以下结论。
（1）本研究中多元散射校正一阶导数预处理方法优于原始数据，相关系数与校正前相比都有了不同程度的提高，确定了678、709、1931、1939、1996和2201 nm波长为诊断有机质含量的敏感波长。筛选的敏感波长与前人研究一致［22,23］。
（2）利用筛选出的波长构建光谱参数，最终构建的光谱参数分别为NDSI(678,709)、NDSI(678,1931)、NDSI(678,2201)、NDSI(709,1939)和NDSI(1939,2201)。建立MLR、SVM回归和RF回归的有机质含量的高光谱反演模型。其中，RF回归模型在三种模型中拟合效果最好。
由于研究区果园的土壤光谱发射率受土壤本身的理化性质和测试环境的干扰，土壤处理可以在一定程度上消除或减少非有机物对土壤光谱的影响因素。以NDSI为基础建立的随机模型是否适用于其他地区的土壤，还有待进一步调查研究。RF对研究区果园的SOM含量预测结果模型精度更高，有必要在更大范围、更多样本的基础上实验，从而确定更实用的SOM含量估算模型，为生产提供理论依据和技术支持。

References

Publishing order | Descend order by publishing year | Descend order by cited within
1
DOTTO A C, DALMOLIN R S D, CATEN A T, et al. A systematic study on the application of scatter-corrective and spectral-derivative preprocessing for multivariate prediction of soil organic carbon by Vis-NIR spectra[J]. Geoderma, 2018, 314: 262-274.

2
冷疏影, 李秀彬. 土地质量指标体系国际研究的新进展[J]. 地理学报, 1999(2): 83-91.

LENG S, LI X. New progress of international research on land quality index system [J]. Journal of Geography, 1999(2): 83-91.

3
姚阔, 郭旭东, 周冬, 等. 高光谱遥感土地质量指标信息提取研究进展[J]. 地理与地理信息科学, 2014, 30(6): 7-12.

YAO K, GUO X, ZHOU D, et al. Advances in researches on hyperspectral remote sensing information extraction of land quality indicators[J]. Geography and Geo-Information Science, 2014, 30(6): 7-12.

4
傅伯杰. 我国生态系统研究的发展趋势与优先领域[J]. 地理研究, 2010, 29(3): 383-396.

FU B. Trends and priority areas in ecosystem research of China[J]. Geographical Research, 2010, 29(3): 383-396.

5
包青岭, 丁建丽, 王敬哲, 等. 基于随机森林算法的土壤有机质含量高光谱检测[J]. 干旱区地理, 2019, 42(6): 1404-1414.

BAO Q, DING J, WANG J, et al. Hyperspectral detection of soil organic matter content based on random forest algorithm[J]. Arid Land Geography, 2019, 42(6): 1404-1414.

6
李冠稳, 高小红, 肖能文, 等. 基于sCARS-RF算法的高光谱估算土壤有机质含量[J]. 发光学报, 2019, 40(8): 1030-1039.

LI G, GAO X, XIAO N, et al. Estimation soil organic matter contents with hyperspectra based on sCARS and RF algorithms[J]. Chinese Journal of Luminescence, 2019, 40(8): 1030-1039.

7
GEORGE K J, KUMAR S, RAJ R A. Soil organic carbon prediction using visible-near infrared reflectance spectroscopy employing artificial neural network modeling[J]. Current Science, 2020, 119(2): 377-381.

8
WEI L, YUAN Z, WANG Z, et al. Hyperspectral inversion of soil organic matter content based on a combined spectral index model[J]. Sensors, 2020, 20(10): 2777.

9
沈兰芝, 高懋芳, 闫敬文, 等. 基于SVR和PLSR的土壤有机质高光谱估测模型研究[J]. 中国农业信息, 2019, 31(1): 58-71.

SHEN L, GAO M, YAN J, et al. Estimation model of soil organic matter based on SVR and PLSR[J]. China Agricultural Informatics, 2019, 31(1): 58-71.

10
国佳欣, 赵小敏, 郭熙, 等. 基于PLSR-BP复合模型的红壤有机质含量反演研究[J]. 土壤学报, 2020, 57(3): 636-645.

GUO J, ZHAO X, GUO X, et al. Inversion of organic matter content in red soil based on PLSR-BP composite model[J]. Acta Pedologica Sinica, 2020, 57(3): 636-645.

11
张智韬, 劳聪聪, 王海峰, 等. 基于FOD和SVMDA-RF的土壤有机质含量高光谱预测[J]. 农业机械学报, 2020, 51(1): 156-167.

ZHANG Z, LAO C, WANG H, et al. Estimation of Desert Soil Organic Matter through hyperspectra based on Fractional-Order Derivatives and SVMDA-RF[J]. Transactions of the CSAM, 2020, 51(1): 156-167.

12
王延仓, 杨秀峰, 赵起超, 等. 二进制小波技术定量反演北方潮土土壤有机质含量[J]. 光谱学与光谱分析, 2019, 39(9): 2855-2861.

WANG Y, YANG X, ZHAO Q, et al. Quantitative inversion of soil organic matter content in Northern Alluvial soil based on binary wavelet transform[J]. Spectroscopy and Spectral Analysis, 2019, 39(9): 2855-2861.

13
王崇红, 陈冬生, 王燕. 烟台市苹果产业布局及结构优化建议[J]. 中国果树, 2019(6): 101-105.

WANG C, CHEN D, WANG Y. Suggestions on optimization of apple industry layout and structure in Yantai city [J]. China Fruits, 2019(6): 101-105

14
鲍士旦. 土壤农化分析[M]. 北京: 中国农业出版社, 1999.

BAO S. Soil agrochemical analysis [M]. Beijing: China Agricultural Press, 1999.

15
洪永胜, 于雷, 耿雷, 等. 应用DS算法消除室内几何测试条件对土壤高光谱数据波动性的影响[J]. 华中师范大学学报(自然科学版), 2016, 50(2): 303-308.

HONG Y, YU L, GENG L, et al. Using direct standardization algorithm to eliminate the effect of laboratory geometric parameters on soil hyperspectral data fluctuate characteristic[J]. Journal of Central China Normal University (Natural Sciences), 2016, 50(2): 303-308.

16
O'ROURKE S M, HOLDEN N M. Determination of soil organic matter and carbon fractions in forest top soils using spectral data acquired from visible-near infrared hyperspectral images[J]. Soil Science Society of America Journal, 2012, 76: 586-596.

17
周萍, 王润生, 阎柏琨, 等. 高光谱遥感土壤有机质信息提取研究[J]. 地理科学进展, 2008(5): 27-34.

ZHOU P, WANG R, YAN B, et al. Extraction of soil organic matter information by hyperspectral remote sensing[J]. Progress in Geography, 2008(5): 27-34.

18
洪永胜, 朱亚星, 苏学平, 等. 高光谱技术联合归一化光谱指数估算土壤有机质含量[J]. 光谱学与光谱分析, 2017, 37(11): 3537-3542.

HONG Y, ZHU Y, SU X, et al. Estimation of soil organic matter content using hyperspectral techniques combined with normalized difference spectral index[J]. Spectroscopy and Spectral Analysis, 2017, 37(11): 3537-3542.

19
崔霞, 宋清洁, 张瑶瑶, 等. 基于高光谱数据的高寒草地土壤有机碳预测模型研究[J]. 草业学报, 2017, 26(10): 20-29.

CUI X, SONG Q, ZHANG Y, et al. Estimation of soil organic carbon content in alpine grassland using hyperspectral data[J]. Acta Prataculturae Sinica, 2017, 26(10): 20-29.

20
于雷, 洪永胜, 周勇, 等. 高光谱估算土壤有机质含量的波长变量筛选方法[J]. 农业工程学报, 2016, 32(13): 95-102.

YU L, HONG Y, ZHOU Y, et al. Wavelength variable selection methods for estimation of soil organic matter content using hyperspectral technique[J]. Transactions of the CSAE, 2016, 32(13): 95-102.

21
韩兆迎, 朱西存, 刘庆, 等. 黄河三角洲土壤有机质含量的高光谱反演[J]. 植物营养与肥料学报, 2014, 20(6): 1545-1552.

HAN Z, ZHU X, LIU Q, et al. Hyperspectral inversion models for soil organic matter content in the Yellow River Delta[J]. Journal of Plant Nutrition and Fertilizers, 2014, 20(6): 1545-1552.

22
GAO L, ZHU X, HAN Z, et al. Spectroscopy-based soil organic matter estimation in brown forest soil areas of the Shandong Peninsula, China[J]. Pedosphere, 2019, 29(6): 810-818.

23
CAO S, ZHU X, LI C, et al. Estimating total nitrogen content in brown soil of orchard based on hyperspectrum[J]. Open Journal of Soil Science, 2017, 7: 203-215.

Options
Outlines

/

〈 〉

  • ISSN 2097-485X（Online）
    ISSN 2096-8094（Print）
    CN 10-1681/S
    CODEN ZNZHD7
    Aboard PDC: C9452
    Authority in Charge: Ministry of Agriculture and Rural Affairs of the People’s Republic of China
    Sponsor: Agricultural Information Institute, Chinese Academy of Agricultural Sciences
  • Address: No.12 Zhongguancun South St.,Haidian District Beijing P.R.China
    Zip Code: 100081
    Telephone: +86 10 82109657
    E-mail: smartag@caas.cn
京ICP备09089781号-37