1 引 言
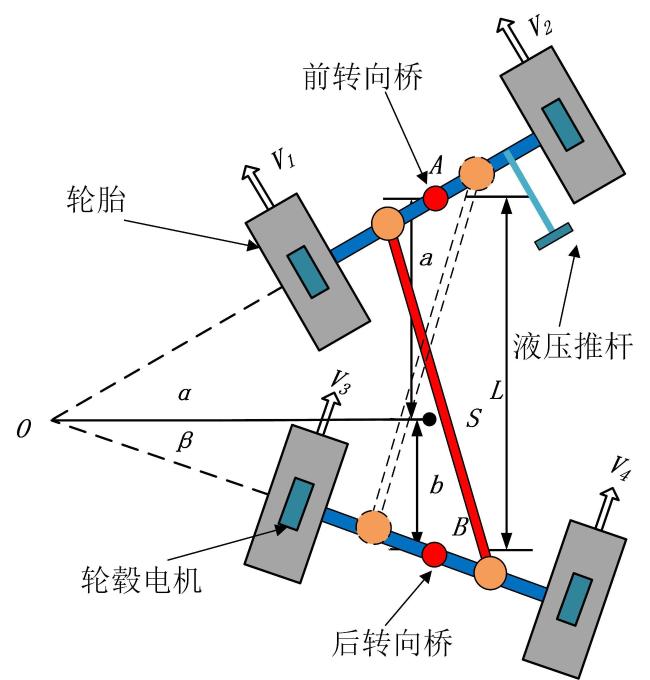
图1 高地隙四轮独立驱动电动喷雾机Fig. 1 High ground clearance four wheel independent drive(4WID) electric sprayer |
2 喷雾机运动学模型
2.1 喷雾机差速转向运动学模型
表1 4WID高地隙喷雾机参数Table 1 Parameters of 4WID high ground clearance sprayer |
| 参数 | 数值 |
|---|---|
| 质量/kg | 2170 |
| 宽度/m | 1.95 |
| 长度/m | 1.7 |
| 轮胎半径/m | 0.47 |
| 驱动轮转动惯量/(kg·m2) | 0.66 |
| 连杆长度/m | 1.49 |
| 喷杆长度/m | 12 |
| 药箱容量/L | 500 |
| 喷施量/(L·min-1) | 5~10 |
| 最大转向角/(°) | 24 |
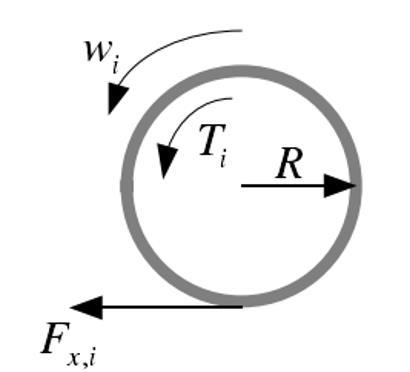
2.2 喷雾机驱动轮动力学模型
2.3 喷雾机的线性时变运动学模型
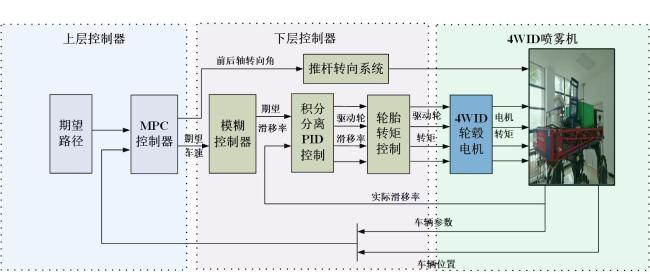
3 LTV-MPC路径跟踪控制
3.1 路径跟踪的MPC
3.2 基于LTV-MPC的控制器设计
3.3 驱动轮滑移率的模糊控制
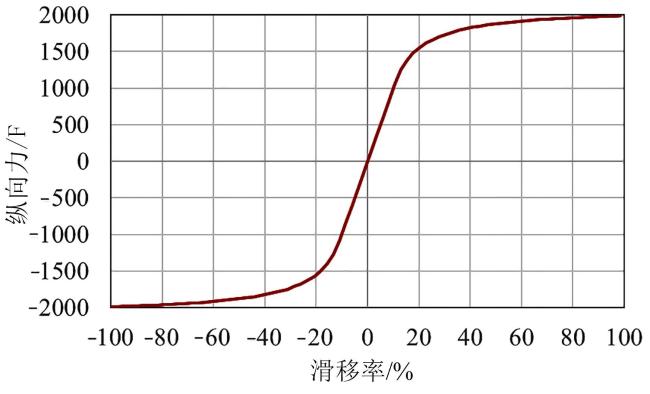
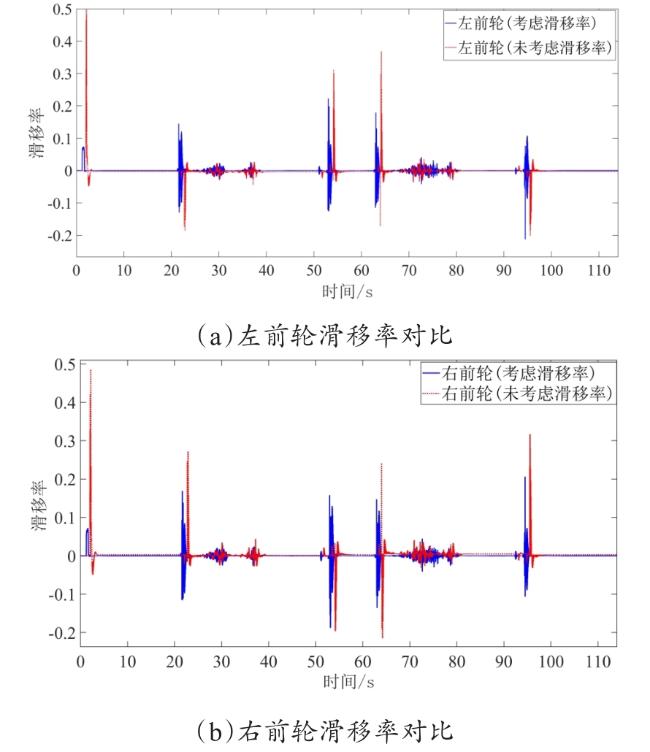
3.3.1 驱动轮滑移率分析
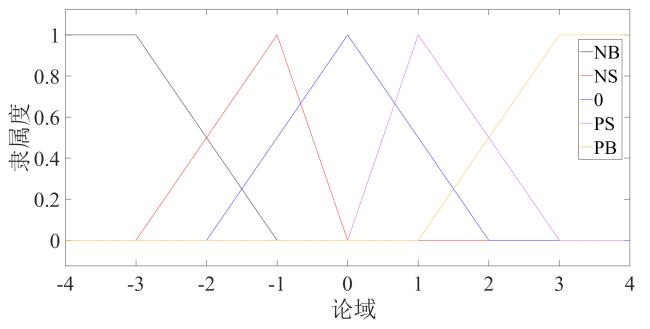
3.3.2 模糊控制器设计
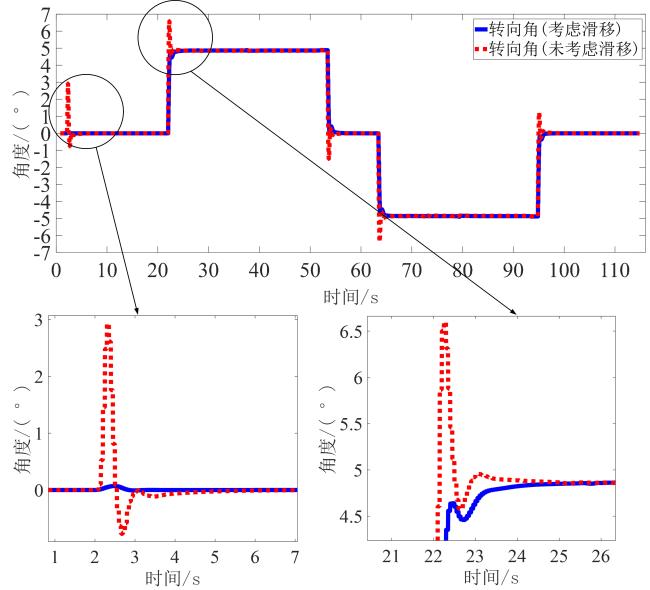
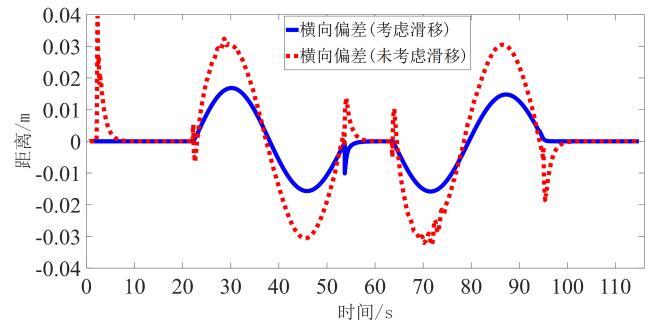
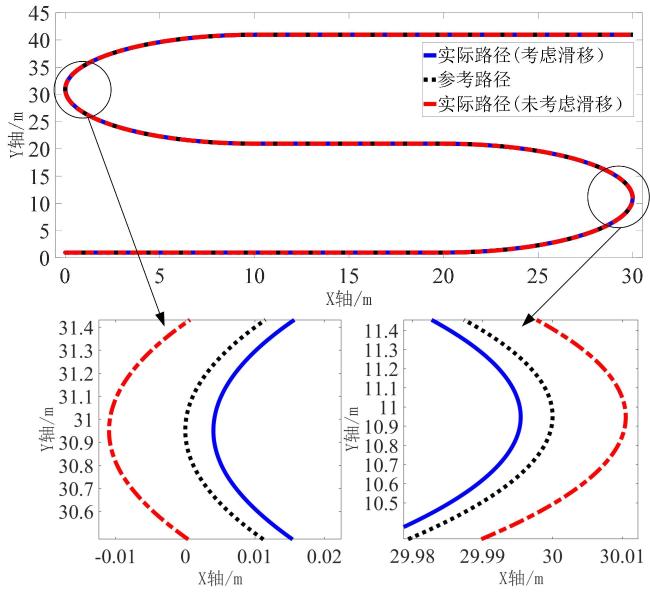
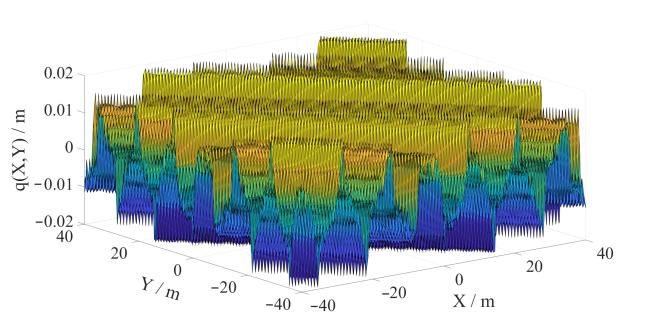
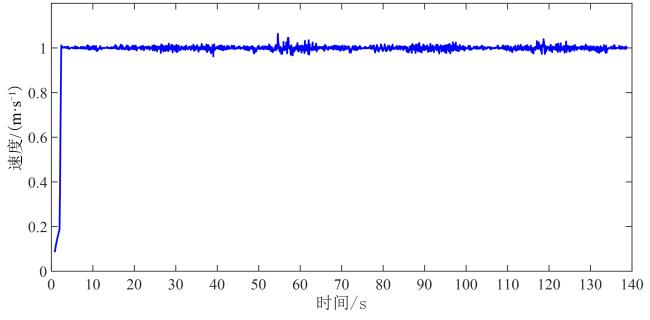
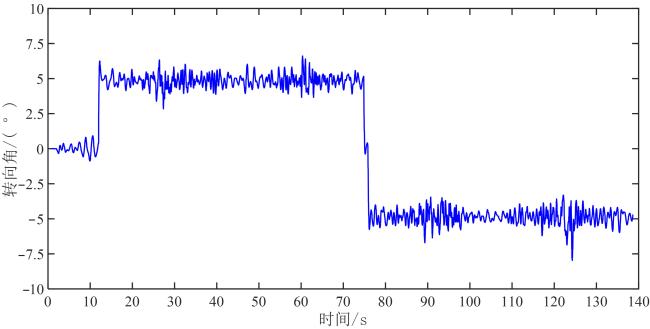
4 仿真结果与分析
表 3 模型预测控制器参数Table 3 Model predictive controller parameters |
| MPC器参数 | 数值 |
|---|---|
| 采样时间/s | 0.05 |
| 控制时域Nc | 30 |
| 预测时域Np | 60 |
| 权重矩阵 Q 权重矩阵 R 车轮转角上限/rad 车轮转角下限/rad 车轮转角增量上限/rad 车轮转角增量下限/rad 松弛因子 | 200× 30× 0.436 -0.436 0.05 -0.05 100 |
表 4 积分分离PID控制器参数Table 4 Integral separation PID controller parameters |
| 控制器参数 | 数值 |
|---|---|
| 采样时间/s | 0.05 |
| 阈值ε | 0.1 |
| 比例控制kp | 5 |
| 积分控制ki | 1.6 |
| 微分控制kd | 0.8 |