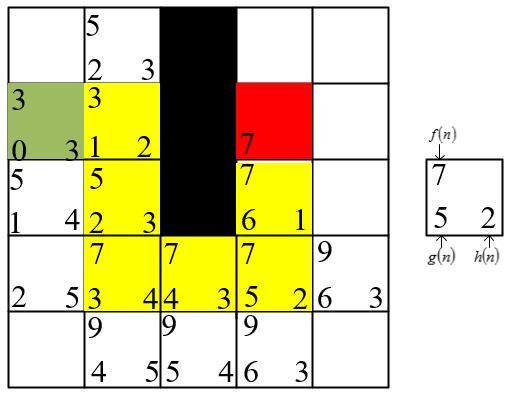
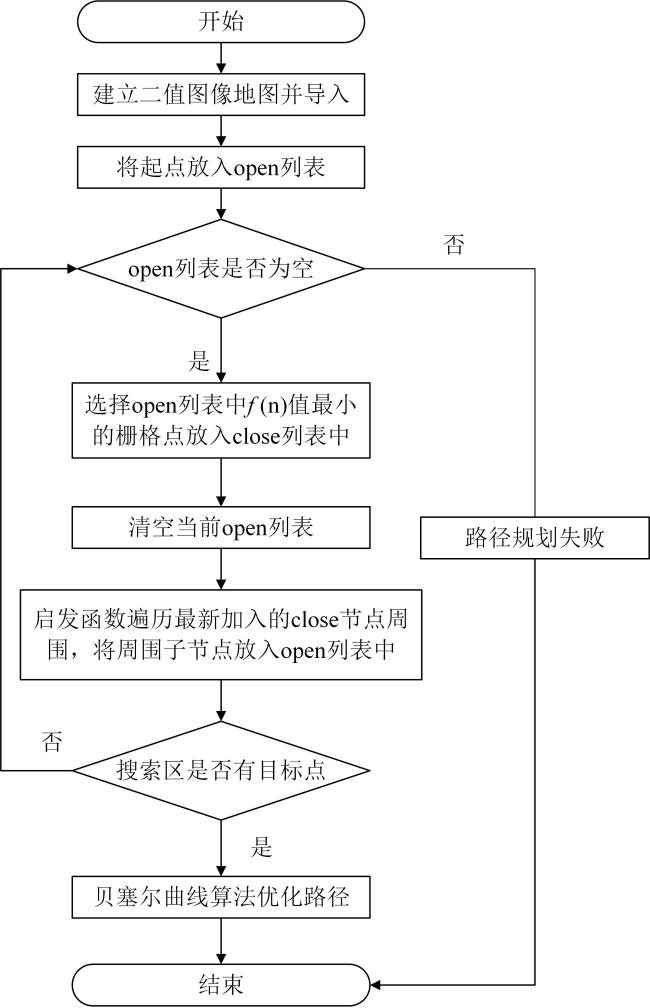
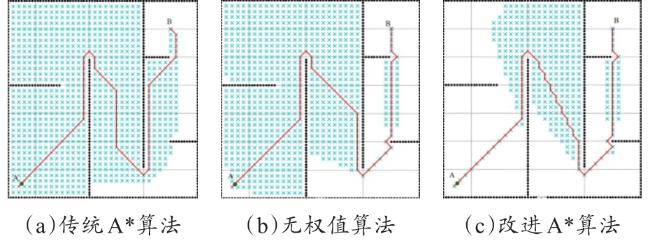
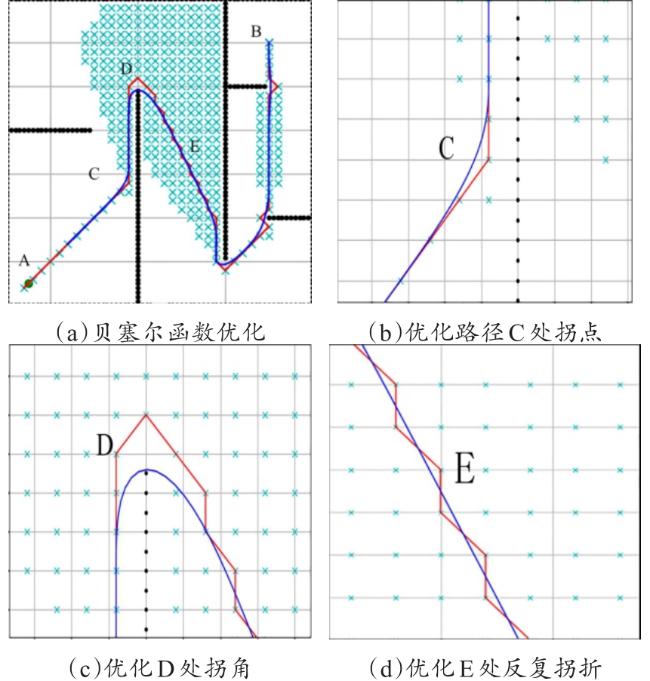
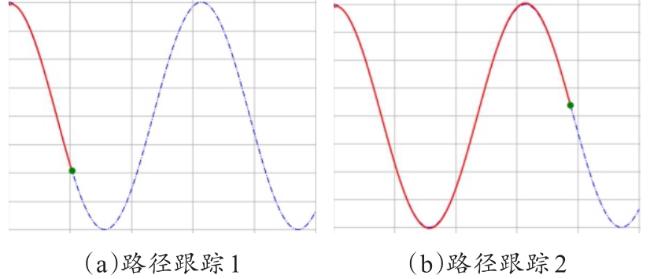
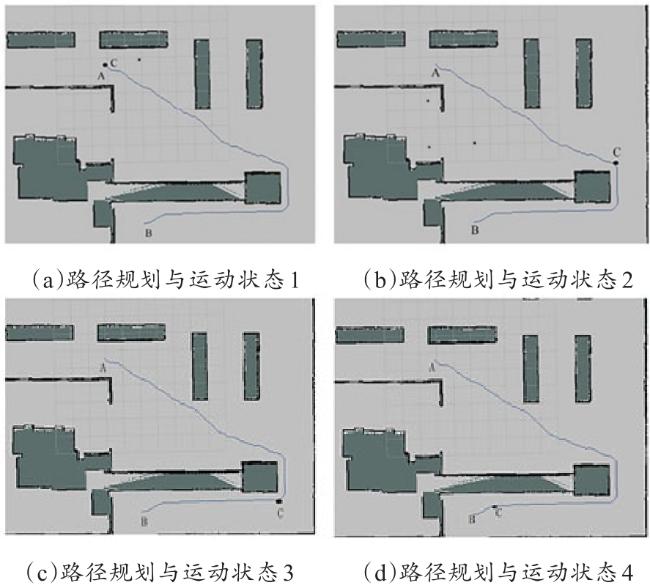
[Objective] A key challenge for the harmless treatment center of sick and dead animal is to prevent secondary environmental pollution, especially during the process of transporting the animals from cold storage to intelligent treatment facilities. In order to solve this problem and achieve the intelligent equipment process of transporting sick and dead animal from storage cold storage to harmless treatment equipment in the harmless treatment center, it is necessary to conduct in-depth research on the key technical problems of path planning and autonomous walking of transport robots. [Methods] A * algorithm is mainly adopted for the robot path planning algorithm for indoor environments, but traditional A * algorithms have some problems, such as having many inflection points, poor smoothness, long calculation time, and many traversal nodes. In order to solve these problems, a path planning method for the harmless treatment of diseased and dead animal using transport robots based on the improved A algorithm was constructed, as well as a motion control method based on fuzzy proportional integral differential (PID). The Manhattan distance method was used to replace the heuristic function of the traditional A * algorithm, improving the efficiency of calculating the distance between the starting and ending points in the path planning process. Referring to the actual location of the harmless treatment site for sick and dead animal, vector cross product calculation was performed based on the vector from the starting point to the target point and the vector from the current position to the endpoint target. Additional values were added and dynamic adjustments were implemented, thereby changing the value of the heuristic function. In order to further improve the efficiency of path planning and reduce the search for nodes in the planning process, a method of adding function weights to the heuristic function was studied based on the actual situation on site, to change the weights according to different paths. When the current location node was relatively open, the search efficiency was improved by increasing the weight. When encountering situations such as corners, the weight was reduced to improve the credibility of the path. By improving the heuristic function, a driving path from the starting point to the endpoint was quickly obtained, but the resulting path was not smooth enough. Meanwhile, during the tracking process, the robot needs to accelerate and decelerate frequently to adapt to the path, resulting in energy loss. Therefore, according to the different inflection points and control points of the path, different orders of Bessel functions were introduced to smooth the planning process for the path, in order to achieve practical application results. By analyzing the kinematics of robot, the differential motion method of the track type was clarified. On this basis, a walking control algorithm for the robot based on fuzzy PID control was studied and proposed. Based on the actual operation status of the robot, the fuzzy rule conditions were recorded into a fuzzy control rule table, achieving online identification of the characteristic parameters of the robot and adjusting the angular velocity deviation of robot. When the robot controller received a fuzzy PID control signal, the angular velocity output from the control signal was converted into a motor rotation signal, which changed the motor speed on both sides of the robot to achieve differential control and adjust the steering of the robot. [Results and Discussions] Simulation experiments were conducted using the constructed environmental map obtained, verifying the effectiveness of the path planning method for the harmless treatment of sick and dead animal using the improved A algorithm. The comparative experiments between traditional A * algorithm and improved algorithm were conducted. The experimental results showed that the average traversal nodes of the improved A * algorithm decreased from 3 067 to 1 968, and the average time of the algorithm decreased from 20.34 s to 7.26 s. Through on-site experiments, the effectiveness and reliability of the algorithm were further verified. Different colors were used to identify the planned paths, and optimization comparison experiments were conducted on large angle inflection points, U-shaped inflection points, and continuous inflection points in the paths, verifying the optimization effect of the Bessel function on path smoothness. The experimental results showed that the path optimized by the Bessel function was smoother and more suitable for the walking of robot in practical scenarios. Fuzzy PID path tracking experiment results showed that the loading truck can stay close to the original route during both straight and turning driving, demonstrating the good effect of fuzzy PID on path tracking. Further experiments were conducted on the harmless treatment center to verify the effectiveness and practical application of the improved algorithm. Based on the path planning algorithm, the driving path of robot was quickly planned, and the fuzzy PID control algorithm was combined to accurately output the angular velocity, driving the robot to move. The transport robots quickly realized the planning of the transportation path, and during the driving process, could always be close to the established path, and the deviation error was maintained within a controllable range. [Conclusions] A path planning method for the harmless treatment of sick and dead animal using an transport robots based on an improved A * algorithm combined with a fuzzy PID motion control was proposed in this study. This method could effectively shorten the path planning time, reduce traversal nodes, and improve the efficiency and smoothness of path planning.