0 引 言
1 问题描述与假设
2 农产品零售市场价格博弈模型建立与竞争策略研究
表1 博弈模型主要字符含义说明表Table 1 Main character meaning description table in game model |
| 字符 | 字符表示含义 |
|---|---|
| | 两家零售企业分别为 (已存在)、 (新进入) |
| v | 消费者对 零售产品的估值 |
| qv | 消费者对 零售产品的估值 |
| k | 信息透明度的提升程度 |
| T | 消费者承受的隐私关注成本 |
| P | 农产品零售商的零售价格 |
| D | 消费者需求 |
| 农产品零售商的利润 |
2.1 农产品对于消费者的效用与需求
2.1.1 农产品效用
2.1.2 消费者需求
表2 两家农产品零售商各种决策选择情况下的需求Table 2 The demands of two agricultural retailers in various decision selection situations |
| 案例 | 条件 | ||
|---|---|---|---|
| AA | |||
| 0 | |||
| BA | |||
| 0 | |||
| AB |
| ||
|
| 0 | ||
|
| 0 | ||
|
| |||
|
| 0 | ||
|
| 0 | ||
| BB | |||
| 0 |
2.2 不同条件下农产品零售商的最优竞争策略
2.2.1 条件为AA时最优竞争策略
表3 案例AA中零售商的最优定价及相应的需求和利润Table 3 The retailer's optimal pricing and corresponding demand and profit in case AA |
| 零售商 | p AA | D AA | π AA |
|---|---|---|---|
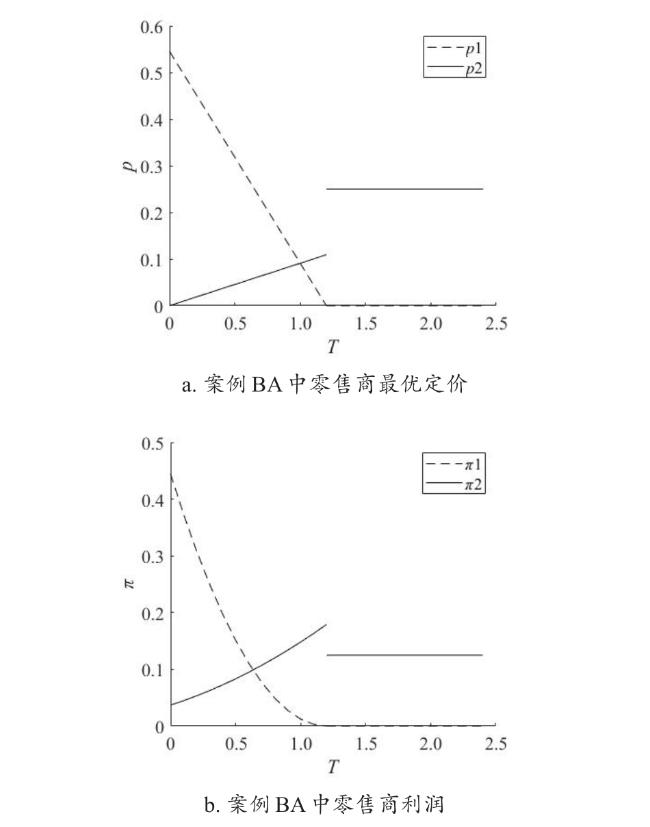
2.2.2 条件为BA时最优竞争策略
表4 案例BA中零售商的最优策略及相应的需求和利润Table 4 Retailer's optimal strategy and corresponding demand and profit in case BA |
| 零售商 | 条件 | ||||
|---|---|---|---|---|---|
| 0 | 0 | 0 | |||
2.2.3 条件为AB时最优策略
表5 案例 AB下零售商的最优策略及其需求和利润Table 5 Retailer's optimal strategy, demand and profit in case AB |
| 零售商 | 条件 | |||
|---|---|---|---|---|
| (0,1) | 0 | 0 | ||
| 0 | 0 | 0 | ||
| (0,1) | 0 | 0 |
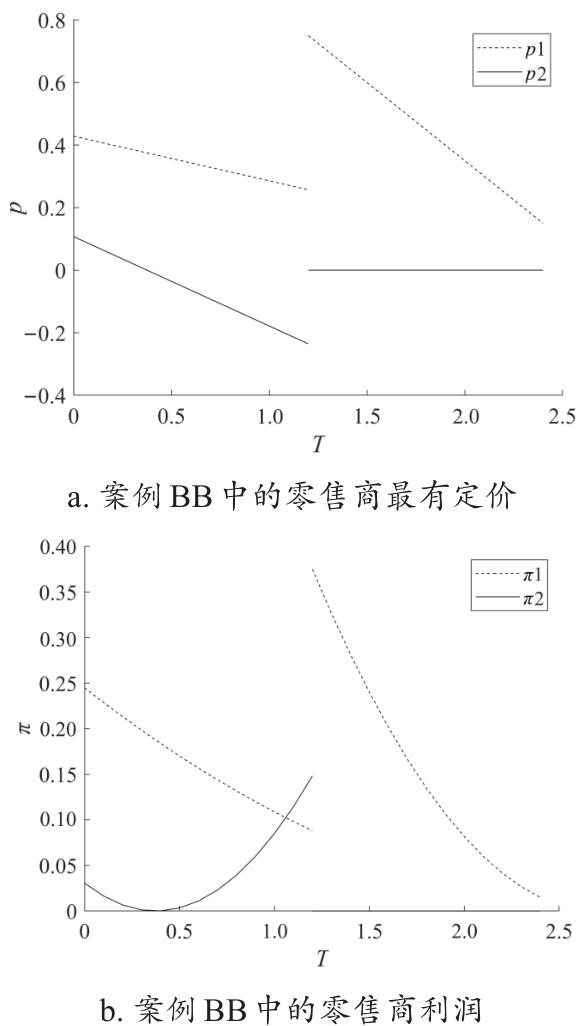
2.2.4 条件为BB时最优策略
表6 案例BB中零售商的最优策略及相应的需求和利润Table 6 Retailer's optimal strategy and corresponding demand and profit in case BB |
| 零售商 | 条件 | |||
|---|---|---|---|---|
| (0,1) | 0 | 0 |
2.3 农产品零售竞争中Stackelber博弈研究
2.3.1 不选择溯源农产品时,对 的影响
2.3.2 选择溯源农产品时,对 的影响
2.3.3 不售卖溯源农产品时,对 的影响
2.3.4 售卖溯源农产品时,对 的影响
2.4 农产品零售商均衡策略选择
3 合作博弈智能合约构建
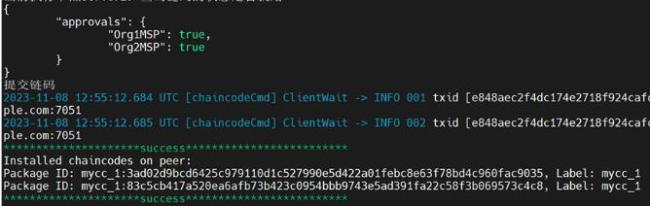
3.1 环境搭建
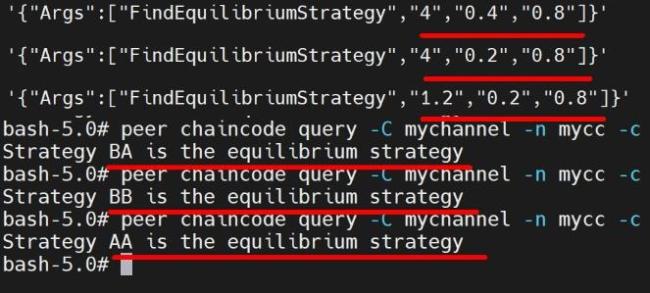
3.2 智能合约构建
表7 合作博弈均衡策略合约Table 7 Cooperative game for determining policies |
| 输入输出 | 伪代码描述 |
|---|---|
| 输入:k值(k>1)、q值(q<1)、零售商 和零售商 对应T值(T<=k) 输出 | Begin T1=根据输入由T1 T5=根据输入由T5 if k×q<1 if T<=T5 || [k>=2/(2‒q)2 && k×q/2<T && T<=k‒sqrt(k)] return“方案BB为均衡策略” else if [k>=2/(2‒q)2 && T5<T && T<=k×q/2] || [k‒sqrt(k)<T && T<=T1] || [k<2/(2‒q)2 && T5<T && T<=T1] return“方案BA为均衡策略” else if [k>=2/(2‒q)2 && T>T1] || [k<2/(2‒q)2 && T>T1] return“方案AA为均衡策略” else if k×q>1 if T<=T5 return“方案BB为均衡策略” else if T5<T && T<=T1 return“方案BA为均衡策略 else if T>T1 return“方案AA为均衡策略” else if k×q=1 if T<=T5 return“方案BB为均衡策略 else if T5<T && T<=T1 return“方案BA为均衡策略” else if {k<=3/2 && 2×k‒(4×k‒1)/sqrt[8×(k‒1)]<=T && T<(16×k 2 ‒16×k+9)/2×(4×k‒1)2} return“方案AB为均衡策略” else if {k<=[2+sqrt(3)]/2 && T>=(16×k 2‒16×k+9)/2×(4×k‒1)2 || k>[2+sqrt(3)]/2 && T>T1} return“方案AA为均衡策略 return“无法得出均衡策略” End |