Tomatoes are a crucial crop, renowned for their high nutritional and health value, providing essential vitamins and trace elements. They also hold significant economic value due to their widespread global cultivation^[1]. Accurate and real-time monitoring of tomato growth and yield is essential for optimizing production, planning export, and evaluating yield-enhancing measures. Existing methods for monitoring and predicting tomato growth primarily include empirical models, mechanistic models, semi-empirical semi-mechanistic models, machine learning models, and deep learning models.

The study of tomato growth models is a vital component of crop modeling. Previous explorations of in this field have categorized based on their establishment methods into mechanistic, semi-mechanistic, and empirical models. Mechanistic models involve mathematical descriptions of plant processes based on known plant mechanisms and are simulated theoretically. Empirical models rely on statistical regularities to study crop growth. Semi-mechanistic models represent a fusion of these two approaches^[2]. Typical mechanistic models include TMOGRO^[3] and TOMSIM, which use a series of equations to reflect the impact of environmental variables— such as indoor temperature, CO₂ concentration, and light on crop growth, morphological changes, and dry matter accumulation. While mechanistic models offer an accurate mathematical depiction based on theoretical simulation, the complexity of actual physiological processes introduces uncertainties and errors that require further investigation^[4]. Empirical models, such as those based on dry matter allocation coefficients, derive parameters through estimation and fitting based on statistical regularities, ensuring model accuracy. Compared to mechanistic models, empirical models are more accessible and widely applicable, with strong practical value. Mechanistic models, while addressing immediate problems, also allow for more in-depth research and exploration, holding significant theoretical value.

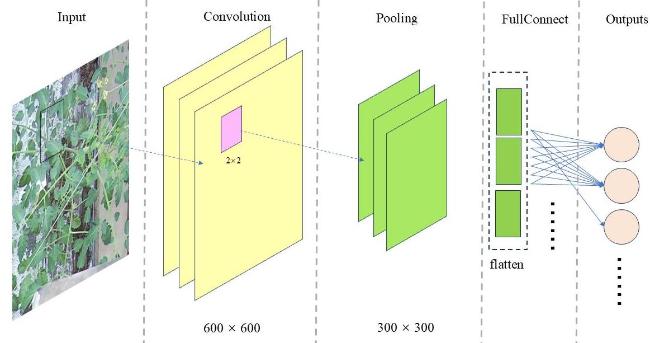
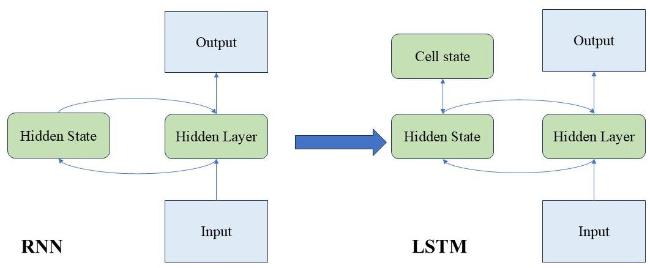
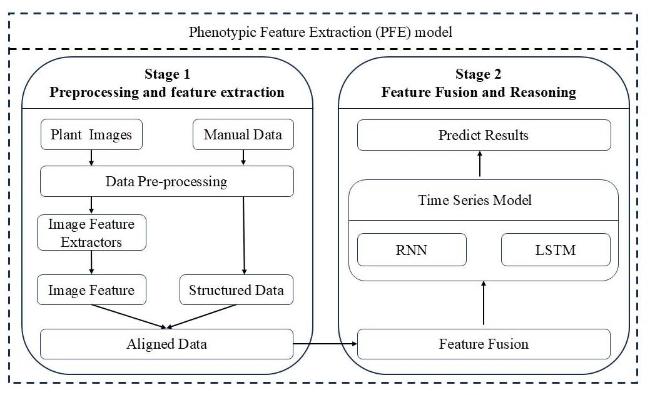
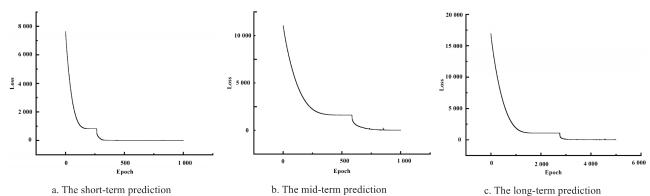
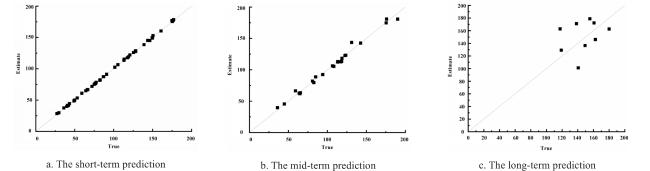
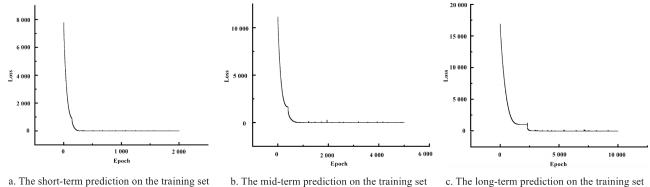
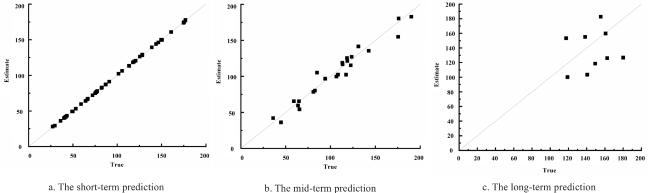
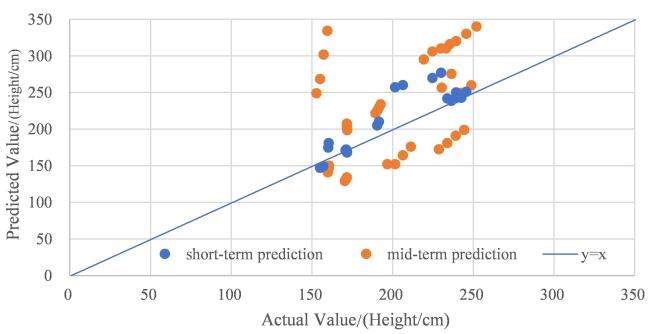
The integration of machine learning with crop models has experienced rapid development, falling within the realm of empirical models and showcasing strong practicality. In the early stages of this integration, research predominantly focused on the application of BP neural networks. Han et al.^[5] successfully developed a principal component analysis-backpropagation neural network (PCA-BPNN) network to predict fruit diameter based on air temperature, air humidity, soil moisture content, and leaf temperature, achieving a maximum error of only 0.075 mm. Focusing on flowering tomatoes, Zhang et al.^[6] established a prediction model for environmental factors and photosynthetic rate using a BP network. The models fitted under various conditions achieved a high accuracy, with an R ² value of 0.96 between the highest predicted and actual values. Additionally, BP network-based models have been successfully applied in predicting winter wheat water consumption^[7], conducting comprehensive evaluation of soil nutrient models^[8], and modeling CO₂ concentration models for the growth of shiitake mushrooms^[9]. All these applications have yielded promising results, highlighting the potential of machine learning in agricultural modeling. Deep learning has revolutionized the integration of machine learning with crop models, particularly through advanced image processing and the incorporation of environmental data. By leveraging deep networks and convolutional methods, deep learning achieves high accuracy in crop growth analysis. For instance, Chen et al.^[10] combined structural and near-infrared image features, identifying random forest as the optimal approach for biomass prediction. Yang et al.^[11] used convolutional neural network (CNN) with random forests and depth maps, thereby reducing the normalized mean square error (NMSE) in lettuce growth predictions. Chandel et al.^[12] demonstrated that GoogleNet excelled in classifying water stress, while Yalcin^[13] used activation maps derived from sunflower images for yield estimation. Beyond image analysis, deep learning also excels when working solely with environmental data. Bali et al.^[14] showed that long short-term memory (LSTM) models outperformed other methods in predicting wheat yield using historical climate data. Nigam et al.^[15] assessed various deep learning models for yield prediction based on temperature and rainfall. Elavarasan and Vincentt^[16] achieved 93.7% accuracy in crop yield prediction with a Q-network model. In tomato yield prediction, De Alwis et al. ^[17] proposed a domain adaptation long short-term memory (DA-LSTM) model that outperformed traditional LSTM, XGBoost Regression (XGBR), and support vector regression (SVR) models. Zhou et al.^[18] integrated the TOMSIM and GreenLight models with deep neural network(DNN) to improve predictions of greenhouse climate-tomato production. Statistics revealed a 30-fold increase in the use of deep learning for crop yield prediction from 2016 to 2020^[19], often surpassing the performance of traditional models^[20]. However, deep learning's reliance on specific datasets limits its transferability between different crops or regions^{[21, 22]}, necessitating extensive localized data to address regional variation and ensure model adaptability.

In recent years, research on plant growth prediction utilizing multi-modal data has predominantly centered on remote sensing information. For instance, Maimaitijiang et al. ^[23] integrated RGB, multispectral, and thermal sensors within a DNN framework to predict soybean grain yield. Their findings indicated that multi-modal fusion within the DNN framework yields relatively stable and reliable prediction results. Similarly, Yang et al.^[24] leveraged multi-source remote sensing data alongside non-remote sensing data (such as temperature and precipitation) to estimate key growth parameters—leaf area index (LAI), aboveground biomass (AGB), leaf nitrogen content (LNC), and soil plant analysis development (SPAD) values—during the early growth stage of canola seedlings. By comparing various model frameworks, including SVR, partial least squares (PLS), BPNN, and neural matrix regression (NMR), they found that models integrating multi-source remote sensing and non-remote sensing data achieved the highest average accuracy. Further advancing this field, Lin et al.^[25] proposed a deep learning model based on multi-modal fusion, utilizing RGB-D images to automatically estimate the fresh weight of lettuce seedlings. The model achieved a root mean square error (RMSE) of 25.3 g and an R² of 0.938 across the entire growth period of lettuce, demonstrating the significant enhancement in prediction accuracy afforded by multi-modal fusion across different growth stages. However, the reliance on remote sensing data is not without limitations. Such data may result in the loss of fine-grained details and is primarily suited for large-scale predictions. Moreover, the use of multispectral and RGB-D data introduces challenges related to convenience and usability, which can hinder practical application. Certainly, there are also simple, user-friendly multi-modal models capable of performing various predictions, such as large language models (LLMs)^[26]. In this study, a deep learning model was employed as a baseline model for comparative analysis. Building upon this foundation, multi-modal data were employed to develop high accuracy models for predicting tomato growth height. Environmental signals, including light and temperature, with specific plant conditions and growth-stage images were entegrated to track plant development. This method effectively synthesizes both phenotypic and temporal features, providing a comprehensive understanding of the interaction between tomato plants and their environment, thereby improving prediction accuracy. A key innovation of this work lies in the use of simple RGB images combined with sensor data, coupled with individualized monitoring of each plant. This approach enables to the capture of more detailed growth phenotype information, resulting in a more granular and precise model for plant growth prediction, which contrasts with the challenges faced by larger-scale, remote sensing-based approaches.

The proposed method utilizes multi-modal data to capture both phenotypic and temporal relationships, which are essential for accurate tomato growth height prediction. Specifically, the method integrates phenotypic features extracted from plant images with temporal patterns derived from environmental factors, such as light and temperature, over time. The key stages of the method include data preprocessing, network training, and performance evaluation. During training, a CNN extractes phenotypic features from the images, while a LSTM captures temporal dependencies within the environmental data. By aligning these two types of features in a joint space, the model achieves comprehensive spatiotemporal fitting, significantly enhancing its ability to model the dynamic interactions between the plant and its environment.

In the training dataset, the leaf area data on the first day (Mean = 208.2, Standard deviation = 68.14, Coefficient of variation(CV) = 32.7%) and plant height data (Mean = 18.6, Standard deviation = 3.1, CV = 16.7%) exhibited a relatively concentrated distribution. In contrast, on the last day, the leaf area data (Mean = 3 113.7, Standard deviation = 1 050.5, CV = 33.7%) and plant height data (Mean = 186.8, Standard deviation = 49.23, CV = 26.3%) demonstrated significantly greater variability. Notably, the standard deviation of the leaf area reached 1 050.5, indicating that leaf area is an unstable metric and may not serve as a reliable indicator of plant growth status. Although plant height was relatively more stable compared to leaf area, its CV increased from 16.7% to 26.3% (CV > 20%), suggesting potential instability in the dataset overall.

However, the training dataset comprised two distinct plant varieties. When analyzing the plant height data of these two varieties separately on the last day, Guanghui 201 exhibited a mean of 149.7, a standard deviation of 29.3, and a CV of 19.5%, while Jinzhu showed a mean of 223.8, a standard deviation of 35.2, and a CV of 15.7%. These CV values fall within an acceptable range, and the variability in plant height decreases when analyzed separately by variety. These variations in leaf area and plant height suggest that the features may influence the accuracy of tomato growth height prediction. Specifically, while leaf area exhibits higher variability and is less stable, plant height shows more stability and can serve as a more reliable predictor. The increased CV in plant height over time indicates some fluctuation that could impact the long-term prediction accuracy. This analysis suggests that integrating both features (leaf area and plant height) into the prediction model, with an emphasis on plant height as a key feature, may enhance the robustness of the growth height prediction, particularly when accounting for the variability across different growth stages.

This study presents a Phenotypic Feature Extraction (PFE) model, which demonstrates significant advantages in predicting tomato growth height using multimodal data. In contrast to unimodal approaches, such as RNN and LSTM models that depend exclusively on either environmental data or images, the PFE model effectively integrates phenotypic and temporal features to construct a unified spatiotemporal representation, thereby significantly improving prediction accuracy.

In contrast to previous studies^{[23, 24]} that primarily use remote sensing and large-scale data, this research leverages easily accessible RGB images and fine-grained environmental sensor data, combined with individualized plant monitoring, to capture more fine-grained crop phenotypic information. This approach addresses the limitations of remote sensing in handling detailed crop characteristics while offering greater applicability and operational simplicity. Aligning with the work of Lin et al.^[25] on predicting lettuce fresh weight using RGB-D images, this study's multimodal integration further investigates the nonlinear interactions between plant growth and environment factors, thereby enabling more rubost and stable predictions under complex conditions.

Furthermore, the findings indicate that the PFE-LSTM model exhibits lower error variation in long-sequence prediction scenarios (e.g., 30-12), consistent with prior research that highlights the role of multimodal data fusion in mitigating overfitting. For instence, Tang et al.^[30] pointed out that multimodal sensor fusion technology can obtain more reliable, informative, and accurate data by extracting and combining multimodal information. Compared to LLMs, the PFE model also demonstrates significant advantages in computational efficiency and interpretability, particularly for tasks involving longer input sequences. Its superior prediction accuracy further validates its potential for applications in precision agriculture.

Despite the promising results, there are some limitations in this study. For instance, it does not explore the applicability of the proposed model across different regions or latitudes. Future studies could expand to larger geographic areas and incorporate additional factors such as topography and climate variability to analyze the spatial dynamics of suitable sowing periods and growth patterns. Such efforts would enhance the generalizability and robustness of the findings.

Future work will focus on developing more granular crop growth models based on multimodal data, capturing dynamic growth changes by incorporating a wider range of multimodal inputs. Additionally, the model structure will be further refined through integration with established crop growth optimization models such as Agricultural Production Systems sIMulator (APSIM) or Decision Support System for Agrotechnology Transfer (DSSAT) to explore the applicability of the PFE model across different crop species, growth stages, and geographic regions. This approach aims to enhance the model's versatility and precision in addressing complex agricultural scenarios.

In this study, deep learning models were employed to predict tomato growth using multimodal data, encompassing environmental factors and plant images. By integrating phenotypic and temporal features, the research aimed to enhance prediction accuracy and analyze the interactions between plant and their environment.

The results showed that the PFE-RNN model achieved the best performance, with a MAPE of 0.81% in short-term (5-2) predictions and 2.66% in medium-term (10-4) predictions, demonstrating its effectiveness in capturing plant growth dynamics. The PFE framework proved particularly valuable by integrating spatial (image) and temporal (environmental) features, enabling accurate and stable predictions.

This study highlights the importance of selecting suitable model architectures and data scales for plant growth prediction. Future work should focus on expanding datasets and exploring advanced temporal models to further improve accuracy and generalization, thereby supporting precision agriculture through improved crop management and sustainability.